Bài 3: Ôn tập chương Mặt nón, mặt trụ, mặt cầu

I. SỰ TẠO THÀNH MẶT TRÒN XOAY

Trong không gian cho mặt phẳng \(\left(P\right)\) chứa đường thẳng \(\Delta\) và đường cong \(\left(C\right)\). Khi quay mặt phẳng \(\left(P\right)\) quanh \(\Delta\) một góc \(360^0\) thì đường cong \(\left(C\right)\) tạo nên một hình được gọi là mặt tròn xoay.

Đường cong \(\left(C\right)\) được gọi là đường sinh của mặt tròn xoay đó. Đường thẳng \(\Delta\) được gọi là trục của mặt tròn xoay.

II. MẶT NÓN TRÒN XOAY

1. Định nghĩa

Trong mặt phẳng \(\left(P\right)\), cho hai đường thẳng \(d\) và \(\Delta\) cắt nhau tại \(O\) và tạo thành góc \(\beta\left(0^o< \beta< 90^o\right)\). Khi quay mặt phẳng \(\left(P\right)\) xung quanh \(\Delta\) thì đường thẳng \(d\) sinh ra một mặt được gọi là mặt nón tròn xoay đỉnh \(O\) (hay mặt nón).

Đường thẳng \(\Delta\) là trục, đường thẳng \(d\) gọi là đường sinh và góc \(2\beta\) gọi là góc ở đỉnh của mặt nón đó.

2. Hình nón tròn xoay và khối nón tròn xoay

Cho tam giác \(OIM\) vuông tại \(I\). Khi quay tam giác đó quanh cạnh góc vuông \(OI\) thì đường gấp khúc \(OIM\) tạo thành một hình gọi là hình nón tròn xoay, gọi tắt là hình nón.

Khối nón tròn xoay (hay gọi tắt là khối nón) là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó.

3. Diện tích xung quanh của khối nón tròn xoay

Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh. Tức là nếu bán kính đáy của hình nón là \(r\), độ dài đường sinh là \(l\) thì diện tích xung quanh của hình nón được tính theo công thức:

\(S_{xq}=\pi rl\)

Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy:

\(S_{tp}=S_{xq}+S_đ=\pi rl+\pi r^2\)

4. Thể tích khối nón tròn xoay

Thể tích \(V\) của khối nón tròn xoay có diện tích đáy \(B\) và chiều cao \(h\) là: 

\(V=\dfrac{1}{3}Bh\)

Như vậy nếu bán kính đáy bằng \(r\) thì \(B=\pi r^2\) nên \(V=\dfrac{1}{3}\pi r^2h\).

III. MẶT TRỤ TRÒN XOAY

1. Định nghĩa

Trong mặt phẳng \(\left(P\right)\) cho hai đường thẳng \(\Delta\) và \(l\) song song với nhau, cách nhau một khoảng bằng \(r\). Khi quay mặt phẳng \(\left(P\right)\) xung quanh \(\Delta\) thì đường thẳng \(l\) sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay (gọi tắt là mặt trụ). Đường thẳng \(\Delta\) gọi là trục, đường thẳng \(l\) là đường sinh và \(r\) là bán kính của mặt trụ đó.

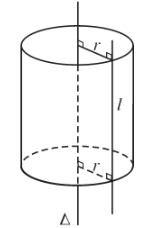
2. Hình trụ tròn xoay và khối trụ tròn xoay

Xét hình chữ nhật \(ABCD\). Khi quay hình đó quanh một đường thẳng chứa một cạnh, chẳng hạn cạnh \(AB\), thì đường gấp khúc \(ADCB\) tạo thành một hình được gọi là hình trụ tròn xoay hay còn được gọi tắt là hình trụ.

Khối trụ tròn xoay (hay khối trụ) là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ đó.

3. Diện tích xung quanh của hình trụ tròn xoay

Diện tích xung quanh của hình trụ tròn xoay bằng tích của chu vi đường tròn đáy và độ dài đường sinh.

Tức là nếu đáy của hình trụ tròn xoay là hình tròn bán kính \(r\), độ dài đường sinh là \(l\) thì diện tích xung quanh của hình trụ đó được tính theo công thức:

\(S_{xq}=2\pi rl\)

 Diện tích toàn phần của hình trụ bằng tổng diện tích xung quanh và diện tích đáy:

\(S_{tp}=S_{xq}+S_đ=2\pi rl+2\pi r^2\)

4. Thể tích khối trụ tròn xoay

Gọi \(V\) là thể tích của khối trụ tròn xoay có diện tích đáy \(B\) và chiều cao \(h\), ta có công thức:

\(V=Bh\)

Như vậy,  nếu bán kính đáy là \(r\) thì \(B=\pi r^2\), suy ra

 \(V=\pi R^2h.\)

IV. MẶT CẦU

1. Mặt cầu

Tập hợp các điểm \(M\) trong không gian cách điểm \(O\) cố định một khoảng không đổi bằng \(r\left(r>0\right)\) được gọi là mặt cầu tâm \(O\) bán kính \(r\).

Kí hiệu: \(S\left(O;r\right)\) hay viết tắt là \(\left(S\right)\). 

Như vậy ta có mặt cầu \(S\left(O;r\right)=\left\{M|OM=r\right\}\).

- Nếu hai điểm \(C,D\) nằm trên mặt cầu \(S\left(O;r\right)\) thì đoạn thẳng \(CD\) được gọi là dây cung của mặt cầu đó.

- Dây cung \(AB\) đi qua tâm \(O\) của mặt cầu được gọi là đường kính của mặt cầu. Khi đó đường kính của mặt cầu bằng \(2r\).

2. Điểm nằm trong và điểm mặt ngoài mặt cầu. Khối cầu

Cho mặt cầu tâm \(O\) bán kính \(r\) và một điểm \(A\) bất kì trong không gian.

- Nếu \(OA=r\) thì ta nói điểm \(A\) nằm trên mặt cầu \(S\left(O;r\right)\) ;

- Nếu \(OA< r\) thì ta nói điểm \(A\) nằm trong mặt cầu \(S\left(O;r\right)\) ;

- Nếu \(OA>r\) thì ta nói điểm \(A\) nằm ngoài mặt cầu \(S\left(O;r\right)\).

Tập hợp các điểm thuộc mặt cầu \(S\left(O;r\right)\) và các điểm nằm trong mặt cầu đó được gọi là khối cầu hoặc hình cầu tâm \(O\) bán kính \(r\).

3. Giao của mặt cầu và mặt phẳng

Cho mặt cầu \(S\left(O;r\right)\) và mặt phẳng \(\left(P\right)\). Gọi \(H\) là hình chiếu của \(O\) lên \(mp\left(P\right)\). Khi đó \(h=OH\) là khoảng cách từ \(O\) đến \(mp\left(P\right)\).

- Trường hợp \(h>r\): Khi đó mặt phẳng \(\left(P\right)\) không có điểm chung với mặt cầu \(S\left(O;r\right)\).

- Trường hợp \(h=r\): Khi đó mặt phẳng \(\left(P\right)\) tiếp xúc với mặt cầu \(S\left(O;r\right)\) tại điểm \(H\).

Điểm \(H\) gọi là tiếp điểm của mặt cầu \(S\left(O;r\right)\) và mặt phẳng \(\left(P\right)\), mặt phẳng \(\left(P\right)\) được gọi là tiếp diện của mặt cầu.

Điều kiện cần và đủ để mặt phẳng \(\left(P\right)\) tiếp xúc với mặt cầu \(S\left(O;r\right)\) tại điểm \(H\) là \(\left(P\right)\) vuông góc với bán kính \(OH\) tại \(H\).

- Trường hợp \(h< r\): Mặt phẳng cắt mặt cầu theo đường tròn tâm \(H\), bán kính \(r'=\sqrt{r^2-h^2}\).

Mặt phẳng đi qua tâm \(O\) của mặt cầu được gọi là mặt phẳng kính của mặt cầu đó.

4. Giao của mặt cầu và đường thẳng

Cho mặt cầu \(S\left(O;r\right)\) và đường thẳng \(\Delta\). Gọi \(H\) là hình chiếu vuông góc của \(O\) lên \(\Delta\) và \(d=OH\) là khoảng cách từ \(O\) tới \(\Delta\).

- Trường hợp \(d>r\):  \(\Delta\) không cắt mặt cầu \(S\left(O;r\right)\).

- Trường hợp \(d=r\):  \(\Delta\) tiếp xúc với mặt cầu \(S\left(O;r\right)\) tại điểm \(H\).

Điểm \(H\) được gọi là điểm tiếp xúc (hay tiếp điểm) của \(\Delta\) và mặt cầu. Đường thẳng \(\Delta\) gọi là tiếp tuyến của mặt cầu.

Điều kiện cần và đủ để đường thẳng \(\Delta\) tiếp xúc với mặt cầu \(S\left(O;r\right)\) tại điểm \(H\) là \(\Delta\) vuông góc với bán kính \(OH\) tại điểm \(H\) đó.

- Trường hợp \(d< r\):  \(\Delta\) cắt mặt cầu \(S\left(O;r\right)\) tại hai điểm phân biệt.

Nhận xét: Người ta chứng minh được rằng:

a) Qua một điểm \(A\) nằm trên mặt cầu \(S\left(O;r\right)\) có vô số tiếp tuyến của mặt cầu đó. Tất cả các tiếp tuyến này đều vuông góc với bán kính \(OA\) của mặt cầu tại \(A\) và đều nằm trong mặt phẳng tiếp xúc với mặt cầu tại điểm \(A\) đó.

b) Qua một điểm \(A\) nằm ngoài mặt cầu \(S\left(O;r\right)\) có vô số tiếp tuyến của mặt cầu đã cho. Các tiếp tuyến này tạo thành một mặt nón đỉnh \(A\). Khi đó độ dài các đoạn thẳng kẻ từ \(A\) đến các tiếp điểm đều bằng nhau.

Chú ý: Người ta nói mặt cầu nội tiếp hình đa diện nếu mặt cầu đó tiếp xúc với tất cả các mặt của hình đa diện, còn nói mặt cầu ngoại tiếp hình đa diện nếu tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu.

Khi mặt cầu nội tiếp (ngoại tiếp) hình đa diện, người ta cũng nói hình đa diện ngoại tiếp (nội tiếp) mặt cầu.

5. Công thức tính diện tích mặt cầu và thể tích khối cầu

Mặt cầu bán kính \(r\) có diện tích là: \(S=4\pi r^2\)

Khối cầu bán kính \(r\) có thể tích là: \(V=\dfrac{4}{3}\pi r^3\)

Chú ý:

a) Diện tích \(S\) của mặt cầu bán kính \(r\) bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.

b) Thể tích \(V\) của mặt cầu bán kính \(r\) bằng thể tích khối chóp có diện tích đáy bằng diện tích mặt cầu và có chiều cao bằng bán kính của khối cầu đó.