Nguyên phân là quá trình tế bào phân chia thành hai tế bào con giống hệt nhau về mặt di truyền.
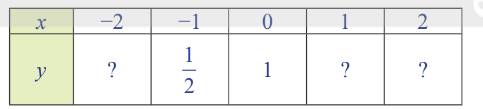
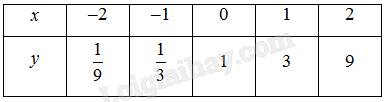
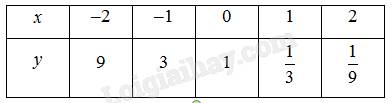
Lập bảng sau đây để tính số tế bào được tạo ra từ một tế bào ban đầu sau những lần nguyên phân.

a) Hoàn thành bảng trên vào vở.
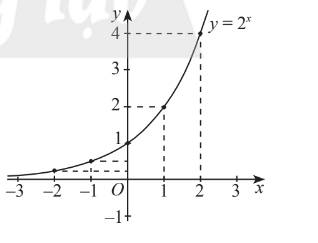
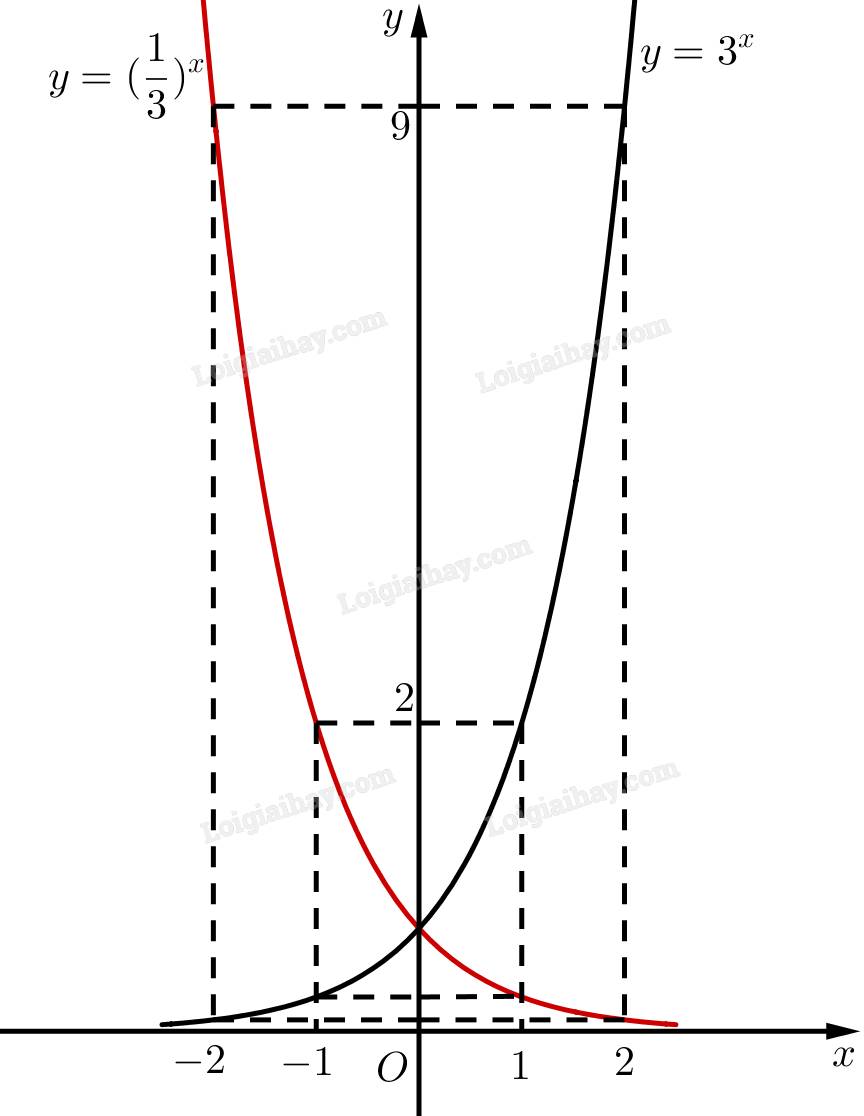
b) Gọi \(y\) là số tế bào được tạo ra từ một tế bào ban đầu sau \(x\left( {x = 0,1,2,...} \right)\) lần nguyên phân. Viết công thức biểu thị \(y\) theo \(x\).