Bài 22. Hình có tâm đối xứng
Nội dung lý thuyết
1. HÌNH CÓ TÂM ĐỐI XỨNG TRONG THỰC TẾ
Quay nửa vòng quanh một điểm
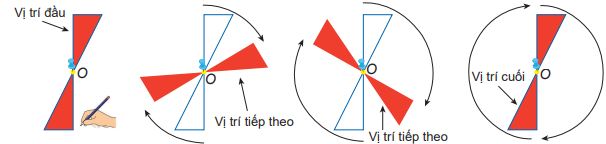
Ta quay nửa vòng một chiếc chong chóng có hai cánh quanh điểm O, khi đó chong chóng lại khớp với vị trí ban đầu.
Ta nói chong chóng này sau khi quay nửa vòng "chồng khít" với chính nó ở vị trí trước khi quay.
Tương tự đối với hình tròn, hình chong chóng bốn cánh, khi quay nửa vòng quanh điểm O ta cũng được hình "chồng khít" với chính nó ở vị trí trước khi quay.
| Hình lúc đầu | Hình sau khi quay nửa vòng |
|
|
|
|
- Hình tròn, chong chóng hai cánh, chong chóng bốn cánh như nói ở trên đều có chung đặc điểm: Mỗi hình có một điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được "chồng khít" với chính nó ở vị trí ban đầu (trước khi quay).
- Những hình như thế gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Ví dụ 1. Những chữ cái nào dưới đây có tâm đối xứng? Chỉ ra tâm đối xứng đó.

Giải:
Chữ cái có tâm đối xứng: N, S, X.
Tâm đối xứng của các chữ cái đó là:

Một số hình có tâm đối xứng trong thực tế
 |
|  |
@1360689@
2. TÂM ĐỐI XỨNG CỦA MỘT SỐ HÌNH PHẲNG
Ví dụ 1. Trong các hình sau: hình bình hành, hình thang cân, hình thoi, hình lục giác đều, hình nào có tâm đối xứng? Chỉ ra tâm đối xứng đó.
Giải:
Các hình có tâm đối xứng: hình bình hành, hình lục giác đều, hình thoi.
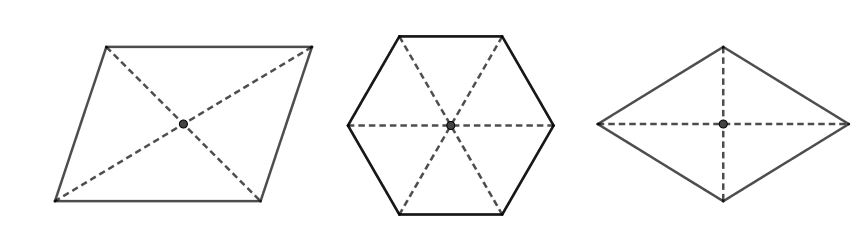
Nhận xét:
- Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Lưu ý: Có những hình có tâm đối xứng và có nhiều trục đối xứng. Cũng có hình không có tâm đối xứng như hình tam giác đều,..
Ví dụ. Hoàn thiện hình sau để thu được hình có tâm đối xứng O.
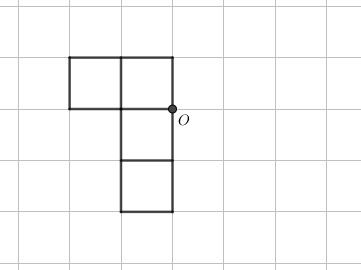
Giải:
Ta được hình có tâm đối xứng O từ hình vẽ trên là:
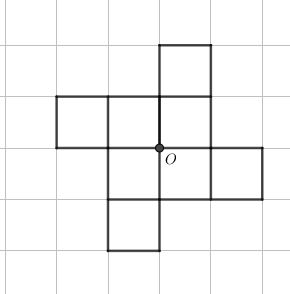
@1361938@@1362367@