Hình 96 minh họa một miếng bìa phẳng có dạng hình tam giác đặt thăng bằng trên đầu ngón tay tại điểm G.
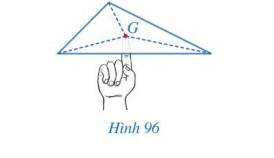
Điểm G được xác định như thế nào?
Hình 96 minh họa một miếng bìa phẳng có dạng hình tam giác đặt thăng bằng trên đầu ngón tay tại điểm G.

Điểm G được xác định như thế nào?
Quan sát Hình 97 và cho biết các đầu mút của đoạn thẳng AM có đặc điểm gì.
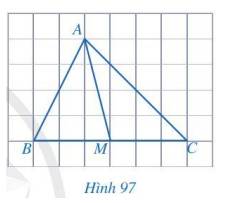
Thảo luận (1)Hướng dẫn giảiCác đầu mút của đoạn thẳng AM: đầu mút A là một đỉnh của tam giác, đầu mút M là trung điểm của cạnh BC trong tam giác ABC.
(Trả lời bởi Hà Quang Minh)
Trong Hình 101, đoạn thẳng HK là đường trung tuyến của những tam giác nào?
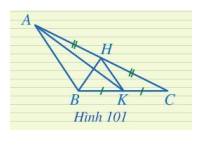
Thảo luận (1)Hướng dẫn giảiĐoạn thẳng HK là đường trung tuyến của tam giác: KAC (đỉnh K và trung điểm H của cạnh AC) và HBC (đỉnh H và trung điểm K của cạnh BC).
(Trả lời bởi Hà Quang Minh)
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 102, cho biết ba đường trung tuyến đó có cùng đi qua một điểm hay không.
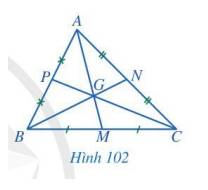
Thảo luận (1)Hướng dẫn giảiBa đường trung tuyến AM, BN, CP của tam giác ABC có cùng đi qua một điểm là điểm G.
(Trả lời bởi Hà Quang Minh)
Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.
Thảo luận (1)Hướng dẫn giải
Ta có G là giao điểm của hai đường trung tuyến QM và RK.
Mà I là trung điểm của QR nên PI cũng là đường trung tuyến trong tam giác PQR.
Vậy PI giao với QM và RK tại G
Do đó, G thuộc PI hay ba điểm P, G, I thẳng hàng.
(Trả lời bởi Kiều Sơn Tùng)
Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 104. Bằng cách đếm số ô vuông, tìm các tỉ số
\(\dfrac{{AG}}{{AM}},\dfrac{{BG}}{{BN}},\dfrac{{CG}}{{CP}}\).
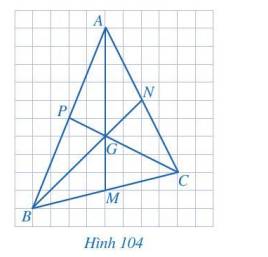
Thảo luận (1)Hướng dẫn giảiTa có:
\(\dfrac{{AG}}{{AM}} = \dfrac{6}{9} = \dfrac{2}{3}\);
\(\dfrac{{BG}}{{BN}} = \dfrac{4}{6} = \dfrac{2}{3}\);
\(\dfrac{{CG}}{{CP}} = \dfrac{4}{6} = \dfrac{2}{3}\).
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:
\(GA + GB + GC = \dfrac{2}{3}(AM + BN + CP)\).
Thảo luận (1)Hướng dẫn giải
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).
(Trả lời bởi Kiều Sơn Tùng)
Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:
a) BM = CN; b) \(\Delta GBC\) cân tại G.
Thảo luận (1)Hướng dẫn giải
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.
(Trả lời bởi Kiều Sơn Tùng)
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:
a) GA = GD;
b) \(\Delta MBG = \Delta MCD\);
c) \(CD = 2GN\).
Thảo luận (1)Hướng dẫn giải
a) G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC.
Suy ra: \(AG = 2GM\). Mà trên tia đối của tia MA lấy điểm D sao cho MD = MG nên \(GD = 2GM\).
Vậy GA = GD (= 2GM).
b) Xét hai tam giác MBG và MCD có:
MB = MC (M là trung điểm cạnh BC)
\(\widehat {GMB} = \widehat {DMC}\)(đối đỉnh)
GM = GD.
Vậy \(\Delta MBG = \Delta MCD\)(c.g.c).
c) \(\Delta MBG = \Delta MCD\) nên BG = CD (2 cạnh tương ứng).
Mà G là trọng tâm tam giác ABC nên \(BG = 2GN\). Mà BG = CD nên \(CD = 2GN\).
(Trả lời bởi Kiều Sơn Tùng)
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:
a) \(\Delta AHB = \Delta AHM\); b) \(AG = \dfrac{2}{3}AB\).
Thảo luận (1)Hướng dẫn giải
a) Xét tam giác AHB và tam giác AHM có:
AH chung;
\(\widehat {AHB} = \widehat {AHM}\)(H là hình chiếu của A lên BC nên \(AH \bot BC\));
HB = HM (H là trung điểm của BM).
Vậy \(\Delta AHB = \Delta AHM\)(c.g.c).
b) \(\Delta AHB = \Delta AHM\)nên AB = AM ( 2 cạnh tương ứng).
G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC. Nên: \(AG = \dfrac{2}{3}AM\).
Mà AB = AM suy ra: \(AG = \dfrac{2}{3}AB\).
(Trả lời bởi Kiều Sơn Tùng)