Bài 1:

\(\widehat{B}=180^0-70^0=110^0\)

\(\widehat{D}=180^0-130^0=50^0\)

Bài 2:

Gọi E là trung điểm của CD
Xét tứ giác ABED có 

AB//ED

AB=ED
DO đó: ABED là hình bình hành

mà AB=AD

nên ABED là hình thoi

mà \(\widehat{BAD}=90^0\)

nên ABED là hình vuông

=>BE vuông góc với DC

Ta có: ABED là hình vuông

nên DB là tia phân giác của góc ADE

=>\(\widehat{BDE}=45^0\)

Xét ΔBDC có

BE là đường cao

BE là đường trung tuyến

Do đó:ΔBDC cân tại B

=>\(\widehat{C}=45^0\)

hay \(\widehat{ABC}=135^0\)

a) Ta có: \(\widehat{B}=120^o,\widehat{A}=90^o\Rightarrow\widehat{C}+\widehat{D}=360^o-\widehat{A}-\widehat{B}=150^o\)

CO, DO là hai tia phân giác góc C và góc D

=> \(\widehat{C_1}+\widehat{D_1}=\frac{1}{2}\widehat{C}+\frac{1}{2}\widehat{D}=\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)=\frac{1}{2}.150^o=75^o\)

=> \(\widehat{COD}=180^o-\left(\widehat{C_1}+\widehat{D_1}\right)=180^o-75^o=105^o\)

b) 

Xét tam giác COD

Ta có: \(\widehat{COD}=180^o-\left(\widehat{C_1}+\widehat{D_1}\right)=180^o-\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)\)

Vì: \(\widehat{C_1}+\widehat{D_1}=\frac{1}{2}\widehat{C}+\frac{1}{2}\widehat{D}=\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)\)

Mặt khác: Xét tứ giác ABCD ta có: \(\widehat{C}+\widehat{D}=360^o-\widehat{A}-\widehat{B}\)

=> \(\widehat{COD}=180^o-\frac{1}{2}\left(360^o-\widehat{A}-\widehat{B}\right)=\frac{1}{2}\widehat{A}+\frac{1}{2}\widehat{B}\)

c) Tương tự ta cũng chứng minh dc:

\(\widehat{BIA}=\frac{1}{2}\widehat{C}+\frac{1}{2}\widehat{D}\)

=> \(\widehat{COD}+\widehat{BIA}=\frac{1}{2}\widehat{A}+\frac{1}{2}\widehat{B}+\frac{1}{2}\widehat{C}+\frac{1}{2}\widehat{D}=\frac{1}{2}\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)=\frac{1}{2}.360^o=180^o\)

=>\(\widehat{FOE}+\widehat{EIF}=180^o\)

=> \(\widehat{OEI}+\widehat{IFO}=180^o\)

Vậy tứ giác EIF có các góc đối bù nhau!

Ta có BAD + ABC + BCD + CDA = 360 độ

ADC + BCD = 360 - 120 - 90 = 150 độ

=> BCO = OCD = 1/2 BCD

=> ADO = ODC = 1/2 ADC

=> ODC + OCD = 1/2 ODC + 1/2 OCD = ODC+OCD/2

=> ODC + OCD = 150 /2 =75 độ

Mà ODC + OCD +DOC = 180 độ

=> DOC = 180 - 75 = 105 độ

B) COD = 180 - (ODC + OCD) 

=> COD = 180 - 1/2ADC + 1/2 BCD

Mà ADC + BCD = 360 - ( BAD + ABC)

COD = 180 - [ 360 - 1/2(BAD + ABC )]

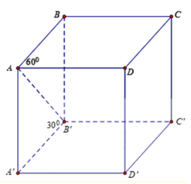
ĐÁP ÁN A

Ta có 

S A B C D = a 2 sin 60 ° = a 2 3 2 A A ' = 30 ° = a 3 3

Thể tích khối hộp là V = A A ' . S A B C D = a 3 3 . a 2 3 2 = a 3 2