Lời giải:

a. Gọi $I(x_0,y_0)$ là điểm cố định mà $(d)$ luôn đi qua. Ta có:

$y_0=(m+1)x_0-m+2, \forall m$

$m(x_0-1)+(x_0+2-y_0)=0, \forall m$

\(\Leftrightarrow \left\{\begin{matrix} x_0-1=0\\ x_0+2-y_0=0\end{matrix}\right.\Leftrightarrow \Rightarrow \left\{\begin{matrix} x_0=1\\ y_0=3\end{matrix}\right.\)

Vậy $I(1,3)$ là điểm cố định mà $d$ luôn đi qua với mọi $m$

b. 

$A(0,a)$ là giao của $(d)$ với trục $Oy$

$B(b,0)$ là giao của $(d)$ với trục $Ox$

Nếu $m=-1$ thì $y=3$

Khi đó, khoảng cách từ $O$ đến $(d)$ là $3$

Nếu $m\neq -1$ thì:

$a=(m+1).0-m+2=-m+2$

$b=\frac{m-2}{m+1}$

Theo hệ thức lượng trong tam giác vuông thì khoảng cách từ $O$ đến $(d)$ là $h$ thì:

$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}$

$=\frac{1}{(m-2)^2}+\frac{(m+1)^2}{(m-2)^2}=\frac{m^2+2m+2}{(m-2)^2}$
$\Rightarrow h=\frac{|m-2|}{\sqrt{m^2+2m+2}}$

9T1

9T1

a) (d) đi qua điểm (1;2)

<=> 2 = k + 1 + k

<=> 1 = 2k

<=> k = 0,5

Vậy k = 0,5 thì (d) đi qua (1;2)

b) Để (d) // đgth y = 2x + 3

\(\Leftrightarrow\hept{\begin{cases}k+1=2\\k\ne3\end{cases}\Leftrightarrow\hept{\begin{cases}k=1\\k\ne3\end{cases}\Rightarrow}k=1}\)

Vậy k =1 thì (d) // đgth y = 2x +3

c) Gọi điểm cố định là (d) đi qua là (x₀;y₀)

Ta có y₀ = ( k +1) x₀ + k

<=> y₀ = kx₀ + x₀+k

<=> y₀ - x₀ - k ( x₀ + 1) = 0 \(\forall\)k

Để pt nghiệm đúng với mọi k <=> \(\hept{\begin{cases}x_0+1=0\\y_0-x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=-1\end{cases}}}\)

Điểm cố định (d) luôn đi qua là ( -1;-1)

y = kx +3 <=>kx+3-y=0 => x=0,y=3

đường thẳng d luôn đi qua một điểm cố định(0;3)

b)khoảgn cách từ gốc toạ độ O tới đường thẳng d bằng căn 2 của x^2+y^2

=>x^2+y^2=4  (1)

Thế y = kx +3, \(x^2+\left(kx+3\right)^2=4\)

\(x^2\left(1+k^2\right)+6kx+5=0\)có nghiệm khi k>=\(\frac{\sqrt{5}}{3}\)

c)

phần c ?

a: Điểm mà (d) luôn đi qua là:

x=0 và y=m*0-3=-3

b: góc BAO=60 độ

=>góc tạo bởi (d) với trục Ox bằng60 độ

=>\(m=tan60=\sqrt{3}\)

c: y=mx-3

=>mx-y-3=0

\(d\left(O;d\right)=\dfrac{\left|0\cdot m+0\cdot\left(-1\right)-3\right|}{\sqrt{m^2+1}}=\dfrac{3}{\sqrt{m^2+1}}\)

Để d lớn nhất thì m^2+1 nhỏ nhất

=>m=0

Gọi điểm cố định mà các đường thẳng (d) đều đi qua P( x o ,  y o ).

Ta có:

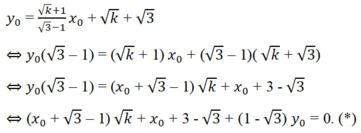
Phương trình (*) nghiệm đúng với mọi giá trị không âm của k , do đó ta có:

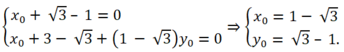
Vậy, với k ≥ 0, các đường thẳng (d) đều đi qua điểm cố định P(1-  3 ;  3  – 1).

a/ Gọi điểm cố định đó là \(N\left(x_0;y_0\right)\) .

Vì (d) đi qua N nên : \(\left(m-2\right)x_0+\left(m-1\right)y_0-1=0\Leftrightarrow m\left(x_0+y_0\right)-\left(2x_0+y_0+1\right)=0\)

Để (d) luôn đi qua N với mọi m thì \(\begin{cases}x_0+y_0=0\\2x_0+y_0+1=0\end{cases}\)

\(\Leftrightarrow\begin{cases}x_0=-1\\y_0=1\end{cases}\) . Vậy điểm cố định đó là N(-1;1)

b/ Gọi \(A\left(\frac{1}{m-2};0\right)\) và \(B\left(0;\frac{1}{m-1}\right)\) là hai điểm thuộc (d)

và A,B lần lượt nằm trên Ox và Oy

Khi đó \(\frac{1}{h^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\)

hay \(\frac{1}{h^2}=\frac{1}{\left(m-1\right)^2}+\frac{1}{\left(m-2\right)^2}\)

Tới đây bạn tìm GTNN của \(\frac{1}{h^2}\) rồi suy ra GTLN của \(h\) nhé :)