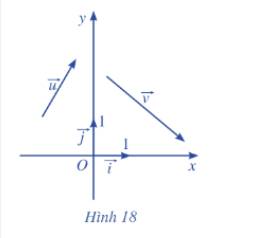
a) Do \(\overrightarrow u  = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v  = \left( {{x_2},{y_2}} \right)\) nên \(\overrightarrow u  = {x_1}\overrightarrow i  + {y_1}\overrightarrow j .\), \(\overrightarrow v  = {x_2}\overrightarrow i  + {y_2}\overrightarrow j .\)

b) +) \(\overrightarrow u  + \overrightarrow v  = \left( {{x_1}\overrightarrow i  + {y_1}\overrightarrow j } \right) + \left( {{x_2}\overrightarrow i  + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i  + {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j  + {y_2}\overrightarrow j } \right) = \left( {{x_1} + {x_2}} \right)\overrightarrow i  + \left( {{y_1} + {y_2}} \right)\overrightarrow j \)

+) \(\overrightarrow u  - \overrightarrow v  = \left( {{x_1}\overrightarrow i  + {y_1}\overrightarrow j } \right) - \left( {{x_2}\overrightarrow i  + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i  - {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j  - {y_2}\overrightarrow j } \right) = \left( {{x_1} - {x_2}} \right)\overrightarrow i  + \left( {{y_1} - {y_2}} \right)\overrightarrow j \)

+) \(k\overrightarrow u  = \left( {k{x_1}} \right)\overrightarrow i  + \left( {k{y_1}} \right)\overrightarrow j \)

c) Tọa độ của các vectơ \(\overrightarrow u  + \overrightarrow v \),\(\overrightarrow u  - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)lần lượt là:

\(\left( {{x_1} + {x_2};{y_1} + {y_2}} \right),\left( {{x_1} - {x_2};{y_1} - {y_2}} \right),\left( {k{x_1},k{y_1}} \right)\)

cái này là j z

a) Tọa độ của vectơ \(\overrightarrow u  + \overrightarrow v  + \overrightarrow w \) là: \(\overrightarrow u  + \overrightarrow v  + \overrightarrow w  = \left( { - 2 + 0 + \left( { - 2} \right);0 + 6 + 3} \right) = \left( { - 4;9} \right)\)

b) Ta có: \(\overrightarrow w  + \overrightarrow u  = \overrightarrow v  \Leftrightarrow \overrightarrow w  = \overrightarrow v  - \overrightarrow u \) nên \(\overrightarrow w  = \left( {0 - \sqrt 3 ; - \sqrt 7  - 0} \right) = \left( { - \sqrt 3 ; - \sqrt 7 } \right)\)

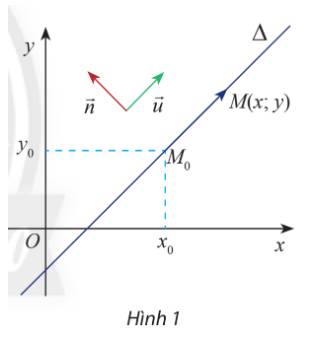
a) Ta có \(\overrightarrow n .\overrightarrow u  = a.b + b.( - a) = 0\)

Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau

b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)

=> luôn cùng phương với vectơ \(\overrightarrow u \)

=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)

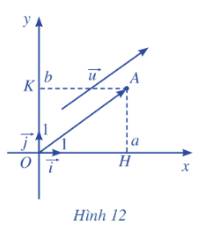
a) Do \(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) nên tọa độ vecto \(\overrightarrow {OA}  = \left( {a;b} \right)\). Vậy tọa độ điểm A là: \(A\left( {a;b} \right)\)

b) TỌa độ điểm H là \(H\left( {a;0} \right)\) nên \(\overrightarrow {OH}  = \left( {a;0} \right)\). Do đó, \(\overrightarrow {OH}  = a\overrightarrow i \)

c) TỌa độ điểm K là \(K\left( {0;b} \right)\) nên \(\overrightarrow {OK}  = \left( {0;b} \right)\). Do đó, \(\overrightarrow {OK}  = b\overrightarrow j \)

d) Ta có: \({\rm{ }}\overrightarrow u  = \overrightarrow {OA} {\rm{ }} = \overrightarrow {OH}  + \overrightarrow {OK}  = a\overrightarrow i  + b\overrightarrow j \) (đpcm)

a) \(\overrightarrow{a}=2\overrightarrow{u}+3\overrightarrow{v}=2\left(3;-4\right)+3\left(2;5\right)=\left(6;-8\right)+\left(6;15\right)\)\(=\left(12;7\right)\).
b) \(\overrightarrow{b}=\overrightarrow{u}-\overrightarrow{v}=\left(3;-4\right)-\left(2;5\right)=\left(1;-9\right)\).
c) Hai véc tơ \(\overrightarrow{c}=\left(m;10\right)\) và \(\overrightarrow{v}\) cùng phương khi và chỉ khi:
\(\dfrac{m}{2}=\dfrac{10}{5}=2\Rightarrow m=4\).

a) Ta có: \(\overrightarrow u  = ({x_1};{y_1}),\;\overrightarrow v  = ({x_2};{y_2}),\;\overrightarrow w  = ({x_3};{y_3}).\)

\(\begin{array}{l} \Rightarrow \overrightarrow v  + \overrightarrow w  = ({x_2};{y_2}) + ({x_3};{y_3}) = \left( {{x_2} + {x_3};{y_2} + {y_3}} \right)\\ \Rightarrow \overrightarrow u .\left( {\overrightarrow v  + \overrightarrow w } \right) = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\end{array}\)

Và: \(\;\overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow w  = \left( {{x_1}.{x_2} + {y_1}.{y_2}} \right) + \left( {{x_1}.{x_3} + {y_1}.{y_3}} \right)\)\( = {x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}.\)

b) Vì \({x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}\)\( = \left( {{x_1}.{x_2} + {x_1}.{x_3}} \right) + \left( {{y_1}.{y_2} + {y_1}.{y_3}} \right)\)\( = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\)

Nên \(\overrightarrow u .\left( {\overrightarrow v  + \overrightarrow w } \right) = \;\overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow w \)

c) Ta có: \(\overrightarrow u  = ({x_1};{y_1}),\;\overrightarrow v  = ({x_2};{y_2})\)

\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow u .\overrightarrow v  = {x_1}.{x_2} + {y_1}.{y_2}\\\overrightarrow v .\overrightarrow u  = {x_2}.{x_1} + {y_2}.{y_1}\end{array} \right.\)\( \Leftrightarrow \;\overrightarrow u .\overrightarrow v  = \overrightarrow v .\overrightarrow u \)

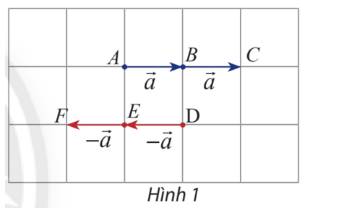
Dựa vào hình 1 ta thấy

Vectơ \(\overrightarrow a  + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)

Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)

a) \(\overrightarrow {MN}  = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)

Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải

\(\overrightarrow {MP}  =  - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)

Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái

b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:

\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a  + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a  + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a  + \overrightarrow b } \right|\)

Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c  = \overrightarrow a  + \overrightarrow b \)

Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)}  = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)}  = \sqrt {10} \)

\( \Rightarrow \left| {2\overrightarrow a  + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a  + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)

a) Tọa độ vectơ \(\overrightarrow u  = \left( {2.\left( { - 1} \right) + 3 - 3.2;2.2 + 1 - 3.\left( { - 3} \right)} \right) = \left( { - 5;14} \right)\)

b) Do \(\overrightarrow x  + 2\overrightarrow b  = \overrightarrow a  + \overrightarrow c  \Leftrightarrow \overrightarrow x  = \overrightarrow a  + \overrightarrow c  - 2\overrightarrow b  = \left( { - 1 + 2 - 2.3;2 + \left( { - 3} \right) - 2.1} \right) = \left( { - 5; - 3} \right)\)

Vậy \(\overrightarrow x  = \left( { - 5; - 3} \right)\)