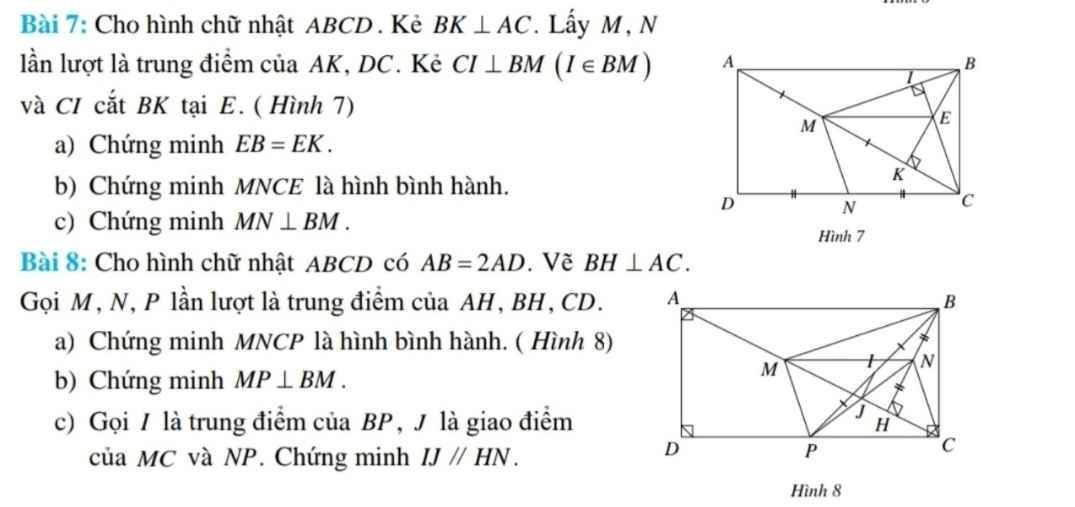
Bài 7:

a: Xét ΔBMC có

CI,BK là các đường cao

CI cắt BK tại E

Do đó: E là trực tâm của ΔBMC

=>ME\(\perp\)BC

Ta có: ME\(\perp\)BC

AB\(\perp\)BC

Do đó: ME//AB

Xét ΔKAB có

M là trung điểm của KA

ME//AB

Do đó: Elà trung điểm của KB

=>EK=EB

b: Xét ΔKAB có

M,E lần lượt là trung điểm của KA,KB

=>ME là đường trung bình của ΔKAB

=>ME//AB và \(ME=\dfrac{AB}{2}\)

ta có: ME//AB

AB//CD

Do đó: ME//CD
mà N\(\in\)CD

nên ME//NC

ta có: \(ME=\dfrac{AB}{2}\)

CD=AB

\(CN=\dfrac{CD}{2}\)

Do đó: ME=CN

Xét tứ giác MECN có

ME//CN

ME=CN

Do đó: MECN là hình bình hành

c: Ta có: MECN là hình bình hành

=>EC//MN

mà EC\(\perp\)BM

nên MN\(\perp\)BM

Bài 8:

Không mất tính tổng quát, giả sử K nằm cùng phía so với A trên nửa mp bờ BC

Do BH song song MN, áp dụng định lý Thales trong tam giác ABH:

\(\dfrac{AB}{AM}=\dfrac{AH}{AG}\)

Do CK song song MN, áp dụng định lý Thales trong tam giác ACK:

\(\dfrac{AC}{AN}=\dfrac{AK}{AG}\)

Mặt khác do BH song song CK (cùng song song MN), áp dụng định lý Thales:

\(\dfrac{OH}{OK}=\dfrac{OB}{OC}=1\) (do O là trung điểm BC)

\(\Rightarrow OH=OK\)

Theo tính chất trọng tâm tam giác: \(AG=\dfrac{2}{3}AO\)

Do đó ta có:

\(\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH}{AG}+\dfrac{AK}{AG}=\dfrac{AH+AK}{AG}=\dfrac{\left(OA-OK\right)+\left(OA+OH\right)}{AG}\)

\(=\dfrac{2AO}{AG}=\dfrac{3AG}{AG}=3\)

Hai tam giác bằng nhau thì đồng dạng

Hai tam giác đồng dạng thì chưa chắc bằng nhau

Hai tam giác đồng dạng chưa chắc sẽ bằng nhau còn khi 2 tam giác bằng nhau thì chắc chắn chúng sẽ đồng dạng. giải thích : Hai Δ có ti số đồng dạng là 1/2 hay 1/3 thì sẽ không bằng nhau tại vì 2 tam giác bằng nhau sẽ có tỉ lệ là 1:1

Hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh tương ứng bằng nhau. ... Vì vậy, nếu hai tam giác bằng nhau, thì cạnh và góc bên thứ ba cũng bằng nhau

Hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh tương ứng bằng nhau. Cơ sở của lý thuyết này là tính chất tổng 3 góc trong tam giác. Theo tính chất tổng góc, tổng ba góc trong một tam giác là 180°. Vì vậy, nếu hai tam giác bằng nhau, thì cạnh và góc bên thứ ba cũng bằng nhau

hfjhfjrjk3jkdjkdbnhnw

Câu 1 : Nếu 2 tam giác vuông có 2 góc nhọn tương ứng bằng nhau thì chúng được gọi là đồng dạng với nhau vì đương nhiên trừ góc vuông ở cả hai tam giác vuông thì góc nhọn còn lại đương nhiên phải bằng nhau.

Câu 2 : Nếu cạnh huyền và cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng. Nếu hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng.

1. đúng 

2. sai

3. sai

4. sai

1. 2 tam giác đều thì đồng dạng 

2. 2 tam vuông thì đồng dạng 

Hai ý đầu chưa rõ 

3. Hai tam giác đồng dạng thì bằng nhau => Sai 

4. Hai tam giác vuông có cạnh huyền bằng nhau thì chúng đồng dạng => Sai 

1: Đúng

2:Sai

3: Sai

4: Sai

Từ câu c suy ra \(\frac{BE}{BD}=\frac{BD}{DF}\)           1

ta có \(B_1=C_1\) (2 góc so le trong)

         \(C_1=D_1\)  (2 góc so le trong)

\(\Rightarrow B_1=D_1\)

Lại có : \(BED=B_1+60\)

             \(BDF=D_1+60\)

\(\Rightarrow BED=BDF\)                   2

Từ 1 và 2 suy ra \(\Delta BDE\infty\Delta DBF\)

bạn ơi câu c cách giải như thế nào vậy