Cho tam giác vuông ABC vuông ở A, AC=20cm; AB=30cm. M là một điểm nằm trên cạnh AC và có tỉ số AM/AC=1/4. Từ M kẻ đường thẳng song song với AB cắt CB tại E. Tính diện tích tam giác AEC?

Những câu hỏi liên quan
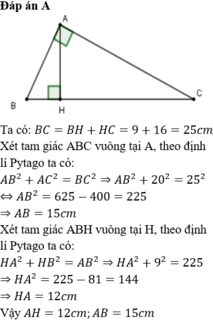
cho tam giác ABC vuông ở A có AC=20cm,kẻ AH vuông góc với BC.Biết BH=9CM,HC=16CM.Tính AB,AH
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9^2+12^2}=15\left(cm\right)\)
Đúng 2
Bình luận (1)
\(BC=BH+HC=9+16=25\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=15\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)
Đúng 2
Bình luận (1)
Ta có :
BC = BH + HC
=> BC = 9 + 16
=> BC = 25 (cm)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+BC^2\) (định lí Py - ta - go)
=> \(25^2=AB^2+20^2\)
=> \(AB^2=225\)
=> AB = 15 (cm)
Xét Δ ABH vuông tại H, có :
\(AB^2=BH^2+AH^2\) (định lí Py - ta - go)
=> \(15^2=9^2+AH^2\)
=> \(AH^2=144\)
=> AH = 12 (cm)
Đúng 1
Bình luận (1)
cho tam giác ABC . Biết BC =52cm , AB=20cm ,AC=48cm
a) CM: tam giác ABC vuông ở A
b) kẻ AH vuông góc với BC . Tính AH
hnay ma nhập nên bài hình nhiều ==
a, Theo định lí Py ta go
Ta cs : \(BC^2=AB^2+AC^2\)
\(52^2=20^2+48^2\)
\(52^2=2704\)
\(52=\sqrt{2704}=52\)
Vậy tam giác ABC vuông tại A ( theo định lí Py ta go đảo )
Vì H nằm giữa B và C
=> HC = HB = 52 . 1/2 = 26cm
Rồi AD định lí Py ta go
a. Áp dụng định lí Py-ta-go đảo
522=202+482
=> 2704 = 400 + 2304
=> 2704 = 2704
=> BC2=AB2+AC2
=> tam giác ABC vuông tại A
b. Diện tích tam giác ABC = \(\frac{1}{2}.AB.AC=\frac{1}{2}20.48=480\)
Diện tích tam giác ABC = \(\frac{1}{2}AH.BC=\frac{1}{2}AH.52\)
=> AH = 18,46
Xem thêm câu trả lời
Cho tam giác ABC vuông ở A có AC=20cm. Kẻ AH vuông góc BC. Biết BH=9cm;HC=16cm. Tính AB,AH
A. AH=12cm;AB=15cm
B. AH=10cm;AB=15cm
C. AH=15cm;AB=12cm
D. AH=12cm;AB=13cm
Lg
*Áp dụng định lý py-ta-go ta có: (Δ AHC)
AC2=AH2+HC2
202=AH2+162
400=AH2+256
AH2=144
AH=√144 =12
*Áp dụng định lý py-ta-go ta có: (Δ AHB)
AB2=AH2+BH2
AB2=122+92
AB2=225
AB=√225 =15
Đúng 0
Bình luận (0)
cho tam giác AB,biết BC=52cm,AB=20cm,AC=48cm.
a,CM: tam giác ABC vuông ở gócA
b,Kẻ AH vuông góc BC.Tính AH
cho tam giác AB,biết BC=52cm,AB=20cm,AC=48cm.
a,CM: tam giác ABC vuông ở gócA
b,Kẻ AH vuông góc BC.Tính AH
a) Theo định lý Pi-ta-go
Ta có : \(\sqrt{20^2+48^2}\)=52
Vậy tam giác vuông tại A.
b
Đúng 0
Bình luận (0)
A. áp dụng định lý pytago trong tam giác abc ta có:
(ab2+ac2)=bc2
=>202+482=522(hợp lí)
=>tam giác abc vuông tại A
B. ta có BH=CH=52:2=26
Xét tam giác ahc có :
CH2+AH2=AC2
=>AH2=AC2-CH2
=>AH2=482-262
=>AH2=1628
=>AH=40.34.....
cho tam giác AB,biết BC=52cm,AB=20cm,AC=48cm.
a,CM: tam giác ABC vuông ở gócA
b,Kẻ AH vuông góc BC.Tính AH
a/ ta có BC2=522=2704
AB2+AC2=20^2+48^2=400+2304=2704
vì 2704=2704 nên BC2=AB2+AC2 hay tam giác ABC vuông tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=15cm, AC=20cm, kẻ đường cao AH của tam giác ABC . Kẻ HM vuông góc AB, HN vuông góc AC. Chứng minh tam giác AMN đồng dạng với tam giác ACB
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN\(\sim\)ΔACB
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Đường cao AH. Cho biết AB=15cm,AC=20cm.
a) Chứng minh AH.BC=AB.AC
b) Tính BC,AH
) Từ H kẻ HE vuông góc với AB ở E và HF vuông góc với AC ở F. Chứng minh tam giác AEF đồng dạng với tam giác ACB
Giải: a) Ta có : \(S_{\Delta ABC}\)= \(\frac{AH.BC}{2}\) (1)
\(S_{\Delta ABC}\)= \(\frac{AB.AC}{2}\) (2)
Từ (1) và (2) suy ra \(\frac{AH.BC}{2}=\frac{AB.AC}{2}\) => AH.BC = AB.AC (Đpcm)
b) Xét t/giác ABC vuông tại A (áp dụng định lí Pi - ta - go)
Ta có: BC2 = AB2 + AC2 = 152 + 202 = 225 + 400 = 625
=> BC = 25
Ta có: AH.BC = AB.AC (cmt)
hay AH. 25 = 15.20
=> AH.25 = 300
=> AH = 300 : 25
=> AH = 12
c) chưa hc
Đúng 0
Bình luận (0)
Cho tam giác ABC : AB = 20cm ; AC = 48cm ; BC = 52cm.
a) CM : tam giác vuông ở A
b) Kẻ AH vuông góc BC . Tính AH
a)
Ta có: BC2=52cm2 = 5704 (cm)
=> AC2+ AB2 =482+202=2304+400=2704 (cm)
=> BC2=AC2+AB2=2704(cm)
=> \(\Delta ABC\) là tam giác vuông ở A
đpcm.
b)
Diện tích tam giác ABC là:
48.20:2=480 (cm2)
Độ dài chiều cao AH là:
480.2:52 = 260/13 (cm)
Vậy.....
a, Ta có : \(BC^2=52^2=2704\)
\(AB^2+AC^2=20^2+48^2=400+2304=2704=52^2\)
Vậy : \(BC^2=AB^2+AC^2\)
Tam giác ABC vuông ở A
b, Ta có : \(S_{ABC}=\frac{1}{2}AB\cdot AC=\frac{1}{2}\cdot20\cdot48=10\cdot48=480\left(cm^2\right)\)
Mặt khác \(S_{ABC}=\frac{1}{2}AH\cdot BC,AH=\frac{2S_{ABC}}{52}=\frac{2\cdot480}{52}\approx18,5\left(cm\right)\)
Phần b bạn dưới làm sai
Cho tam giác ABC vuông ở A có AC=20cm,BC=25cm,đường cao AH với H € BC . Tính BH,CH,AH
Theo định lý Pytago
\(AB^2+AC^2=BC^2\\ \Rightarrow AB=\sqrt{25^2-20^2}=15\left(cm\right)\)
Tam giác ABC vuông tại A , AH đg cao
\(AB.AC=AH.BC\\ \Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{20.15}{25}=12\left(cm\right)\)
\(AB^2=BH.BC\\ \Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
\(AC^2=CH.BC\\ \Rightarrow HC=\dfrac{AC^2}{BC}=\dfrac{20^2}{25}=16\left(cm\right)\)
Đúng 1
Bình luận (0)
ΔACB vuông tại A
=>\(AC^2+AB^2=BC^2\)
=>\(AB^2=25^2-20^2=225\)
=>\(AB=\sqrt{225}=15\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{15^2}{25}=9\left(cm\right)\\CH=\dfrac{20^2}{25}=16\left(cm\right)\\AH=\dfrac{15\cdot20}{25}=12\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)