cần cách trình bày của hai câu này ạ
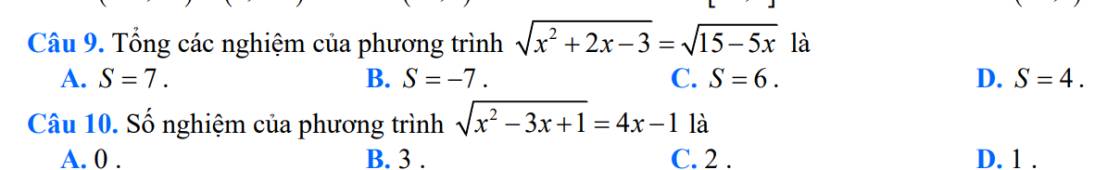
chỉ em cách trình bày bài này với ạ
(7x-1)(3-2x)<0
Em cần cách trình bày ạ
<=> 7x-1>0 và 3-2x<0 hoặc 7x-1<0 và 3-2x>0
<=> x>1/7 và x>3/2 hoặc x<1/7 và x<3/2
<=> x>3/2 hoặc x<1/7
Vậy với x>3/2 hoặc x<1/7 thì thỏa mãn đề bài
(những chữ "hoặc" và chữ "và" bạn có thể thay bằng dấu ngoặc vuông và ngoặc nhọn nhé!!!)
Have a good day!!!
cần trình bày câu này ạ
Trình bày cách giải mấy câu này giúp mình với ạ :((( khó quá


15.
\(\Delta'=m^2+m-2>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
Đáp án B
16.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\dfrac{\pi}{4}< \dfrac{a}{2}< \dfrac{\pi}{2}\Rightarrow\dfrac{\sqrt{2}}{2}< sin\dfrac{a}{2}< 1\Rightarrow\dfrac{1}{2}< sin^2\dfrac{a}{2}< 1\)
\(sina=\dfrac{3}{5}\Leftrightarrow sin^2a=\dfrac{9}{25}\Leftrightarrow4sin^2\dfrac{a}{2}.cos^2\dfrac{a}{2}=\dfrac{9}{25}\)
\(\Leftrightarrow sin^2\dfrac{a}{2}\left(1-sin^2\dfrac{a}{2}\right)=\dfrac{9}{100}\Leftrightarrow sin^4\dfrac{a}{2}-sin^2\dfrac{a}{2}+\dfrac{9}{100}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2\dfrac{a}{2}=\dfrac{1}{10}< \dfrac{1}{2}\left(loại\right)\\sin^2\dfrac{a}{2}=\dfrac{9}{10}\end{matrix}\right.\)
\(\Rightarrow sin\dfrac{a}{2}=\dfrac{3\sqrt{10}}{10}\)
17.
Áp dụng công thức trung tuyến:
\(AM=\dfrac{\sqrt{2\left(AB^2+AC^2\right)-BC^2}}{2}=\dfrac{\sqrt{201}}{2}\)
18.
\(\Leftrightarrow x^2+2x+4>m^2+2m\) ; \(\forall x\in\left[-2;1\right]\)
\(\Leftrightarrow m^2+2m< \min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)\)
Xét \(f\left(x\right)=x^2+2x+4\) trên \(\left[-2;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-2;1\right]\) ; \(f\left(-2\right)=4\) ; \(f\left(-1\right)=3\) ; \(f\left(1\right)=7\)
\(\Rightarrow\min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)=f\left(1\right)=3\)
\(\Rightarrow m^2+2m< 3\Leftrightarrow m^2+2m-3< 0\)
\(\Rightarrow-3< m< 1\Rightarrow m=\left\{-2;-1;0\right\}\)
Đáp án C
19. Hình đa giác là bát giác đều như hình vẽ

\(S=8S_{OAB}=8.\dfrac{1}{2}.IB.OA=4.y_B.x_A=4.\dfrac{\sqrt{2}}{2}.1=2\sqrt{2}\)
Cả 4 đáp án đều không chính xác?
20.
\(M\in\Delta\Rightarrow a+b+1=0\Rightarrow b=-a-1\Rightarrow M\left(a;-a-1\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AM}=\left(a+1;-a-4\right)\\\overrightarrow{BM}=\left(a-1;-a-2\right)\end{matrix}\right.\)
\(AM+BM=\sqrt{\left(a+1\right)^2+\left(-a-4\right)^2}+\sqrt{\left(-a-2\right)^2+\left(a-1\right)^2}\)
\(AM+BM\ge\sqrt{\left(a+1-a-2\right)^2+\left(-a-4+a-1\right)^2}=\sqrt{26}\)
Dấu "=" xảy ra khi:
\(\left(a+1\right)\left(a-1\right)=\left(-a-4\right)\left(-a-2\right)\Leftrightarrow a=-\dfrac{3}{2}\Rightarrow b=\dfrac{1}{2}\)
\(\Rightarrow ab=-\dfrac{3}{4}\)
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!

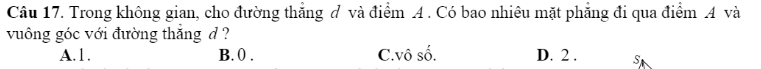
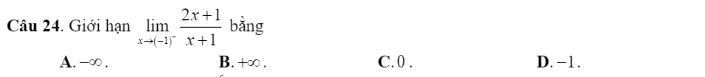

2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...
Bạn nào giải giúp mình hai câu này vs ạ , trình bày hộ mình với , mình cám ơn ạ
22/ \(\omega A=8\pi\)
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Leftrightarrow A^2=3,2^2+\dfrac{\left(4,8\pi\right)^2}{\omega^2}\)
\(\Leftrightarrow\omega^2A^2=3,2^2\omega^2+23,04\pi^2\Leftrightarrow64\pi^2=3,2^2.\omega^2+23,04\pi^2\Leftrightarrow\omega=2\pi\left(rad/s\right)\)
\(\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{2\pi}{2\pi}=1\left(Hz\right)\Rightarrow D.1Hz\)
23/ \(\omega A=20;\omega^2A=80\Rightarrow\left\{{}\begin{matrix}\omega=4\left(rad/s\right)\\A=5cm\end{matrix}\right.\)
\(\Rightarrow v=\omega\sqrt{A^2-x^2}=4.\sqrt{5^2-4^2}=12\left(cm/s\right)\Rightarrow A.12cm/s\)
giúp em giải bài này ạ trung bình cộng của hai số bằng 35 số bé bằng 0,75 số lớn tìm hai số đó mong anh chị giúp em cả cách trình bày ạ
Tổng 2 số là: 35x2 = 70
Số bé là: (70 -0,75) : 2 = 34,625
Số lớn là: 34,625 + 0,75 = 35,375
Đáp số tự ghi nhé
Tổng của hai số là:
35x2=70
Thấy: 0,75=3/4
Gía trị 1 phần là:
70:(3+4)=10
Số lớn là:
10x4=40
Số bé là:
10x3=30
ĐS: SL: 40
SB: 30
Giải thích và trình bày suy nghĩ về câu:
"Gái thương chồng, đương đông buổi chợ
Trai thương vợ, nắng quái chiều hôm".
(- Trình bày ngắn gọn, rõ ràng).
MN GIÚP E BÀI NÀY VỚI Ạ. E ĐANG CẦN GẤP LẮM Ạ.
“Câu tục ngữ phản ánh mức độ khác nhau trong tình yêu thương vợ chồng. Người con gái luôn luôn thương yêu chồng bằng tình yêu đậm đà, mặn mà, đầy đặn khác nào “đương đông buổi chợ”. Còn tình cảm của người con trai chỉ đôi lúc nhưng mãnh liệt như cái “nắng quái chiều hôm” vậy.
Tham Khảo
“Câu tục ngữ phản ánh mức độ khác nhau trong tình yêu thương vợ chồng. Người con gái luôn luôn thương yêu chồng bằng tình yêu đậm đà, mặn mà, đầy đặn khác nào “đương đông buổi chợ”. Còn tình cảm của người con trai chỉ đôi lúc nhưng mãnh liệt như cái “nắng quái chiều hôm” vậy. Nắng quái chiều hôm tuy ngắn ngủi nhưng sức nóng, sức cháy bỏng của ánh nắng xiên khoai này thật là ghê gớm”;
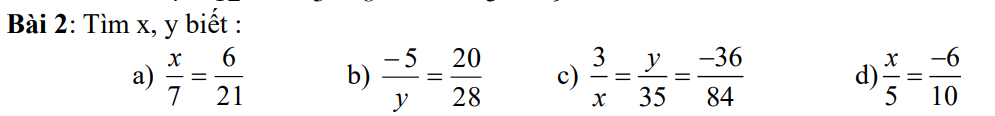 biết kết quả rồi nhưng ko biết cách trình bày ạ, chỉ mik cách trình bày câu A thôi ạ
biết kết quả rồi nhưng ko biết cách trình bày ạ, chỉ mik cách trình bày câu A thôi ạ
\(\dfrac{x}{7}\) = \(\dfrac{6}{21}\) \(\Rightarrow\) \(\dfrac{x}{7}\) = \(\dfrac{2}{7}\) \(\Rightarrow\) \(\dfrac{x.7}{7}\) = \(\dfrac{7.2}{7}\) \(\Rightarrow\) \(x\) = \(\dfrac{7.2}{7}\) \(\Rightarrow\) \(x\) = \(2\)
\(\dfrac{x}{7}=\dfrac{6}{21}\)
Thì x.21=7.6
x.21=42
x=42:21
x=2
Vậy x=2
ai trả lời hộ mik câu này với ạ 57296 chia cho 54 bằng bao? nhiêu và cách trình bày sao cho đúng ạ mik cảm ơn mn rất nhiều !!!