Bài 2 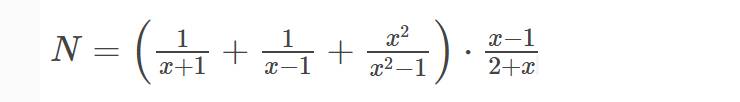
a) viết đkxđ của biểu thức N.
b) Rút gọn biểu thức N
c) Tính giá trị của biểu thức N khi |x|=2

Những câu hỏi liên quan
Cho biểu thức: P và Q (ĐKXĐ: )1. Tính giá trị của biểu thức P khi 2. Rút gọn biểu thức Q.Tìm các số hữu tỉ a để biểu thức M P.Q có giá trị nguyên
Đọc tiếp
Cho biểu thức: P =  và Q =
và Q =  (ĐKXĐ:
(ĐKXĐ: ![]() )
)
1. Tính giá trị của biểu thức P khi ![]()
2. Rút gọn biểu thức Q.
Tìm các số hữu tỉ a để biểu thức M = P.Q có giá trị nguyên
Bài 10: Cho biểu thức:A=3x^2+6x+12/x^3-8
a, Tìm ĐKXĐ của A
b, Rút gọn A
c, Tính giá trị của biểu thức tạix=2021/1010
\(a,ĐK:x\ne2\\ b,A=\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3}{x-2}\\ c,x=\dfrac{2021}{1010}\Leftrightarrow A=\dfrac{3}{\dfrac{2021}{1010}-\dfrac{2020}{1010}}=\dfrac{3}{\dfrac{1}{1010}}=3030\)
Đúng 1
Bình luận (0)
Bài 4: Cho biểu thức M (với x) a) Rút gọn M b) Tính giá trị của biểu thức M với x - 3Bài 5. Cho hai biểu thức: A và B a) Tính giá trị của biểu thức A khi x 5b) Rút gọn biểu thức Bc) Biết P A.B, tìm các số tự nhiên x để P ∈ Z
Đọc tiếp
Bài 4: Cho biểu thức M = ![]() (với x
(với x![]() )
)
a) Rút gọn M
b) Tính giá trị của biểu thức M với x = - 3
Bài 5. Cho hai biểu thức: A = ![]() và B =
và B = ![]()
a) Tính giá trị của biểu thức A khi x = 5
b) Rút gọn biểu thức B
c) Biết P = A.B, tìm các số tự nhiên x để P ∈ Z
cho biểu thức P=\(\dfrac{3x^2+6x+12}{x^3-8}\)
a) Tìm ĐKXĐ của P
b) Rút gọn biểu thức P
c) Tính giá trị của P với x=\(\dfrac{4001}{2000}\)
a, P xác định khi \(x^3-8\ne0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2x+4\right)\ne0\)
\(\Leftrightarrow x\ne2\left(\text{Vì }x^2+2x+4>0\right)\)
b, \(P=\dfrac{3x^2+6x+12}{x^3-8}=\dfrac{3\left(x^2+2x+4\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{3}{x-2}\)
c, \(x=\dfrac{4001}{2000}\Rightarrow P=\dfrac{3}{\dfrac{4001}{2000}-2}=6000\)
Đúng 1
Bình luận (0)
Bài 3. Cho biểu thức : B = 1/(2sqrt(x) - 2) - 1/(2sqrt(x) + 2) + (sqrt(x))/(1 - x) A = (1 - (5 + sqrt(5))/(1 + sqrt(5)))((5 - sqrt(5))/(1 - sqrt(5)) - 1)
a) Tính A
b) Tìm ĐKXĐ rồi rút gọn biểu thức B;
c) Tính giá trị của B với x = 9
d) Tìm giá trị của x để |B| = A
a: \(A=\left(1-\dfrac{5+\sqrt{5}}{1+\sqrt{5}}\right)\left(\dfrac{5-\sqrt{5}}{1-\sqrt{5}}-1\right)\)
\(=\left(1-\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\right)\left(\dfrac{-\sqrt{5}\left(1-\sqrt{5}\right)}{1-\sqrt{5}}-1\right)\)
\(=\left(1-\sqrt{5}\right)\left(-1-\sqrt{5}\right)\)
\(=\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)=5-1=4\)
b: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >1\end{matrix}\right.\)
\(B=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\)
\(=\dfrac{1}{2\left(\sqrt{x}-1\right)}-\dfrac{1}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=-\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=-\dfrac{2}{\sqrt{x}+1}\)
c: Khi x=9 thì \(B=\dfrac{-2}{\sqrt{9}+1}=\dfrac{-2}{3+1}=-\dfrac{2}{4}=-\dfrac{1}{2}\)
d: |B|=A
=>\(\left|-\dfrac{2}{\sqrt{x}+1}\right|=4\)
=>\(\dfrac{2}{\sqrt{x}+1}=4\) hoặc \(\dfrac{2}{\sqrt{x}+1}=-4\)
=>\(\sqrt{x}+1=\dfrac{1}{2}\) hoặc \(\sqrt{x}+1=-\dfrac{1}{2}\)
=>\(\sqrt{x}=-\dfrac{1}{2}\)(loại) hoặc \(\sqrt{x}=-\dfrac{3}{2}\)(loại)
Đúng 2
Bình luận (0)
Bài 1: Rút gọn biểu thức D sqrt{16x^4}-2x^2+1Bài 2: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng điều kiện xác định”e) E dfrac{2sqrt{x}}{sqrt{x}+3} ĐKXĐ: xge0Bài 3: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng hằng đẳng thức ”B 1-sqrt{x^2-2x+2}Bài 4: Cho P dfrac{4sqrt{x}+10}{2sqrt{x}-1}left(xge0;xnedfrac{1}{4}right). Tính tổng các giá trị x nguyên để biểu thức P có giá trị nguyên
Đọc tiếp
Bài 1: Rút gọn biểu thức D = \(\sqrt{16x^4}-2x^2+1\)
Bài 2: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng điều kiện xác định”
e) E = \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}\) ĐKXĐ: \(x\ge0\)
Bài 3: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng hằng đẳng thức ”
B = \(1-\sqrt{x^2-2x+2}\)
Bài 4: Cho P = \(\dfrac{4\sqrt{x}+10}{2\sqrt{x}-1}\left(x\ge0;x\ne\dfrac{1}{4}\right)\). Tính tổng các giá trị x nguyên để biểu thức P có giá trị nguyên
Bài 1:
Ta có: \(D=\sqrt{16x^4}-2x^2+1\)
\(=4x^2-2x^2+1\)
\(=2x^2+1\)
Đúng 0
Bình luận (0)
Bài 2: Cho biểu thức 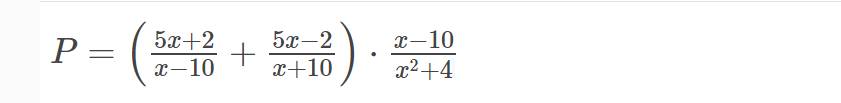
a) tìm điều kiện xác định của P
b) Rút gọn biểu thức P
c) Tính giá trị của P khi x=2/5
a) ĐKXĐ: \(x\ne\pm10\)
b) \(P=\left(\dfrac{5x+2}{x-10}+\dfrac{5x-2}{x+10}\right)\cdot\dfrac{x-10}{x^2+4}\left(x\ne\pm10\right)\)
\(=\left[\dfrac{\left(5x+2\right)\left(x+10\right)}{\left(x-10\right)\left(x+10\right)}+\dfrac{\left(5x-2\right)\left(x-10\right)}{\left(x-10\right)\left(x+10\right)}\right]\cdot\dfrac{x-10}{x^2+4}\)
\(=\dfrac{5x^2+52x+20+5x^2-52x+20}{\left(x-10\right)\left(x+10\right)}\cdot\dfrac{x-10}{x^2+4}\)
\(=\dfrac{10x^2+40}{x+10}\cdot\dfrac{1}{x^2+4}\)
\(=\dfrac{10\left(x^2+4\right)}{\left(x+10\right)\left(x^2+4\right)}\)
\(=\dfrac{10}{x+10}\)
c) Thay \(x=\dfrac{2}{5}\) vào \(P\), ta được:
\(P=\dfrac{10}{\dfrac{2}{5}+10}=\dfrac{25}{26}\)
\(\text{#}Toru\)
Đúng 3
Bình luận (0)
Cho biểu thức với . a) Rút gọn biểu thức ; b) Tìm điều kiện của để ; c) Tìm các giá trị nguyên của để có giá trị nguyên; d)* Với , hãy tìm giá trị lớn nhất của . Bài 8: Cho biểu thức ; với . a) Tính giá trị biểu thức khi . b) Rút gọn biểu thức . c) So sánh với 1. d) Tìm để có giá trị nguyên.
cho biểu thức
A=(2a^2/a^2−1−a/a+1+a/a−1)
a)tìm đkxđ của a để biểu thức A xác định
b)rút gọn biểu thức A
c)tìm các giá trị nguyên của a để biểu thức A có giá trị nguyên




















