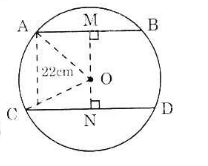
Cho đường tròn tâm O đường kính AB=60cm dây MN=40cm vẽ dây CD//MN và cách MN 20cm. Tính CD

Những câu hỏi liên quan
Cho đường tròn tâm O bán kính 25cm, dây AB bằng 40cm. Vẽ dây CD song song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.
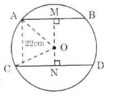
Kẻ OM ⊥ AB, ON ⊥ CD.
Ta thấy M, O, N thẳng hàng. Ta có:
![]()
Áp dụng định lí Pitago trong tam giác vuông AMO có:
OM2 = OA2 – AM2 = 252 – 202 = 225
=> OM = √225 = 15cm
=> ON = MN – OM = 22 – 15 = 7 (cm)
Áp dụng định lí Pitago trong tam giác vuông CON có:
CN2 = CO2 – ON2 = 252 – 72 = 576
=> CN = √576 = 24
=> CD = 2CN = 48cm
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính 25cm, dây AB bằng 40cm. Vẽ dây CD song song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.
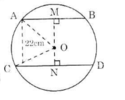
Kẻ OM ⊥ AB, ON ⊥ CD.
Ta thấy M, O, N thẳng hàng. Ta có:
![]()
Áp dụng định lí Pitago trong tam giác vuông AMO có:
O M 2 = O A 2 – A M 2 = 25 2 – 20 2 = 22 2
=> OM = √225 = 15cm
=> ON = MN – OM = 22 – 15 = 7 (cm)
Áp dụng định lí Pitago trong tam giác vuông CON có:
C N 2 = C O 2 – O N 2 = 25 2 – 7 2 = 576
=> CN = √576 = 24
=> CD = 2CN = 48cm
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, bán kính 25cm, dây AB bằng 40cm. Vẽ dây CD song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD?
Kẻ \(OM\perp AB , ON\perp CD\)
Ta thấy M, O, N thẳng hàng. Ta có:
\(AM=\frac{1}{2}AB=20cm ; MN=22cm\)
Áp dụng định lí Pitago trong tam giác vuông AMO có:
OM2 = OA2 – AM2 = 252 – 202 = 225
=> OM = \(\sqrt{225}\) = 15cm
=> ON = MN – OM = 22 – 15 = 7 (cm)
Áp dụng định lí Pitago trong tam giác vuông CON có:
CN2 = CO2 – ON2 = 252 – 72 = 576
=> CN = \(\sqrt{576}\) = 24
=> CD = 2CN = 48cm
Cho đường tròn tâm (O; R) và hai dây AB, CD song song với nhau biết AB = 30cm, CD = 40cm, khoảng cách giữa AB và CD là 35cm. Tính bán kính R của đường tròn tâm O.
Trong 1 đường tròn tâm O, cho 2 dây AB và CD song song với nhau. Biết AB=30cm; CD=40cm; khoảng cách giữa AB và CD là 35cm. Tính bán kính đường tròn
Cho đường tròn tâm O bán kính R,dây AB = R.căn 3 .Vẽ đường kính CD vuông góc AB(C thuộc cung AB lớn).Trên cung AC lấy M.Vẽ dây AN//CM.Tính MN
Bài 14 (trang 106 SGK Toán 9 Tập 1)
Cho đường tròn tâm $O$ bán kính $25$cm, dây $AB$ bằng $40$cm. Vẽ dây $CD$ song song với $AB$ và có khoảng cách đến $AB$ bằng $22$cm. Tính độ dài dây $CD$.
Kẻ OM ⊥ AB, ON ⊥ CD.
Ta thấy M, O, N thẳng hàng. Ta có:
Áp dụng định lí Pitago trong tam giác vuông AMO có:
OM2 = OA2 – AM2 = 252 – 202 = 225
=> OM = √225 = 15cm
=> ON = MN – OM = 22 – 15 = 7 (cm)
Áp dụng định lí Pitago trong tam giác vuông CON có:
CN2 = CO2 – ON2 = 252 – 72 = 576
=> CN = √576 = 24
=> CD = 2CN = 48cm
Ta tính được khoảng cách từ đến bằng cm. Gọi là giao điểm của và . Do nên . Ta có:
(cm)
Từ đó tính được cm
Ta tính được khoảng cách từ đến bằng cm. Gọi là giao điểm của và . Do nên . Ta có:
(cm)
Từ đó tính được cm.
Xem thêm câu trả lời
Trong 1 đường tròn tâm O bán kính 25cm, 2 dây AB và CD song song với nhau. Biết AB=40cm, CD=48cm. Tính khoảng cách giữa 2 dây ấy.
*, Kẻ OH vuông AB, H \(\in\)AB
=> H là trung điểm AB
=> HB = AB/2 = 40/2 = 20 cm
Theo định lí Pytago tam giác OBH vuông tại H
\(OH=\sqrt{OB^2-HB^2}=15\)cm
*, Kẻ OT vuông CD, T \(\in\)CD
=> T là trung điểm CD
=> TD = DC/2 = 48/2 = 24 cm
Theo định lí Pytago tam giác ODC vuông tại T
\(OT=\sqrt{OD^2-DT^2}=7\)cm
Đúng 1
Bình luận (0)
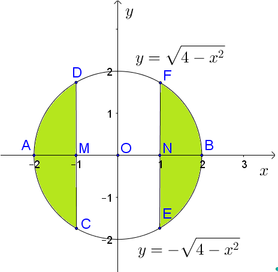
Cho đường tròn tâm O(0;0) đường kính AB 4. Trên AB lấy hai điểm M,N đối xứng với nhau qua O sao cho MN 2. Qua M, N kẻ hai dây cung CD và EF cùng vuông góc với AB. Tính diện tích hình phẳng giới hạn bởi đường tròn và hai dây cung CD, EF (phần không chứa điểm O). A.
S
4
π
3
−
3
B.
S
4
π
−...
Đọc tiếp
Cho đường tròn tâm O(0;0) đường kính AB = 4. Trên AB lấy hai điểm M,N đối xứng với nhau qua O sao cho MN = 2. Qua M, N kẻ hai dây cung CD và EF cùng vuông góc với AB. Tính diện tích hình phẳng giới hạn bởi đường tròn và hai dây cung CD, EF (phần không chứa điểm O).
A. S = 4 π 3 − 3
B. S = 4 π − 2 3
C. S = 8 π 3 − 2 3
D. S = 4 π 3 + 2 3