Câu 9 làm tính nhân a m= (-2x3y).x2-2y+1

Những câu hỏi liên quan
tính giá trị biểu thức: Q=x3+2x3y+2xy+2y+2023, biết x+2y-1=0
\(x+2y-1=0\Rightarrow x+2y=1\)
Q = \(x^3\) + 2\(x^2\)\(y\) + 2\(xy\) + 2\(y\) + 2023
Q = \(x^2\) (\(x\) + 2\(y\)) + 2\(xy\) + 2\(y\) + 2023
Q = \(x^2\)\(\times1\) + 2\(xy\) + 2\(y\) + 2023
Q = \(x\)(\(x\) + 2y) + 2y + 2023
Q = \(x\) \(\times\) 1 + 2y + 2023
Q = 1 + 2023
Q = 2024
Đúng 2
Bình luận (0)
1.Tính
a, -2x3y(2x2- 3y+ 5yz)
b, (x +3) (x2 +3x -5)
c, (-x2+6x2-26x+21): (2x-3)
a) (1- x2). ( 4x+5/x-1 - 9/x-1)b. x2 + xy - 2x - 2y Câu 5. Cho hàm số: y (2m+1)x - 3 a. Với m3. Tính f (-3); f(0) b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số. c. Vẽ đồ thị hàm số với m 1 d. Tìm điều kiện để hàm số là hàm bậc nhất. e. Tìm m để hàm số song song với đường thẳng y 5x+1
Đọc tiếp
a) (1- x2). ( 4x+5/x-1 - 9/x-1)
b. x2 + xy - 2x - 2y
Câu 5. Cho hàm số: y = (2m+1)x - 3
a. Với m=3. Tính f (-3); f(0)
b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số.
c. Vẽ đồ thị hàm số với m= 1
d. Tìm điều kiện để hàm số là hàm bậc nhất.
e. Tìm m để hàm số song song với đường thẳng y= 5x+1
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
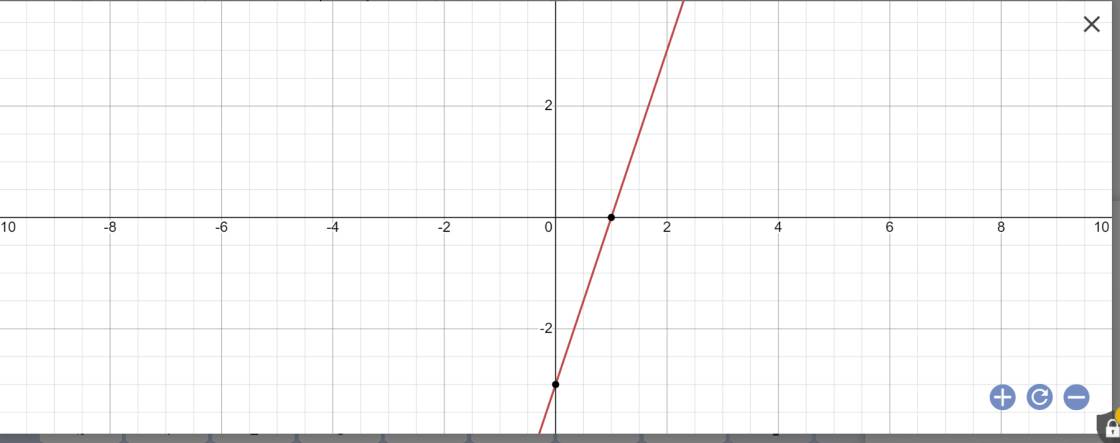
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
Đúng 0
Bình luận (0)
Toán vận dụng: phân tích đa thức: x4-y4+2x3y-2xy3 thành nhân tử (x+y).(x2-y2)
\(x^4-y^4+2x^3y-2xy^3\)
\(=\left(x^2+y^2\right)\left(x^2-y^2\right)+2xy\left(x^2-y^2\right)\)
\(=\left(x^2-y^2\right)\left(x^2+y^2+2xy\right)\)
\(=\left(x-y\right)\left(x+y\right)\left(x+y\right)^2\)
\(=\left(x-y\right)\left(x+y\right)^3\)
Đúng 0
Bình luận (1)
\(x^4-y^4+2x^3y-2xy^3\\ =\left(x^2\right)^2-\left(y^2\right)^2+2xy\left(x^2-y^2\right)\\ =\left(x^2-y^2\right)\left(x^2+y^2\right)+2xy\left(x^2-y^2\right)\\ =\left(x^2-y^2\right)\left(x^2+y^2+2xy\right)\\ =\left(x-y\right)\left(x+y\right)\left(x+y\right)^2\\ =\left(x-y\right)\left(x+y\right)^3\)
Đúng 0
Bình luận (2)
Cho hai đa thức sau:
P = −x3y−xy+x2+4x3y+2xy+1−x3y−xy+x2+4x3y+2xy+1
Q = x3y−8xy−5+2x3y+9x2+4−10x2x3y−8xy−5+2x3y+9x2+4−10x2
a) Thu gọn đa thức P và Q. Xác định bậc của đa thức P và Q sau khi thu gọn.
b) Tính A = P + Q và B = P - Q
c) Tính giá trị của đa thức A khi x=1x=1 và y=−1y=−1
Tính:
+ 12x6y3 : 4x3y
+ (x+1)(x2 – x + 1)
+ 2x2y(x2+ 3xy)
Phân tích đa thức thành nhân tử:
+ 4x2y + 6 xy2 -8xy
+x2 – 9
+ x2 – 4 +xy – 2y
+x2 - 7x +10
Tìm x biết:
+x2-x( x-2) = 2
+( x-2)2 + x -2= 0
\(1,\\ 12x^6y^3:4x^3y=3x^3y^2\\ \left(x+1\right)\left(x^2-x+1\right)=x^3+1\\ 2x^2y\left(x^2+3xy\right)=3x^4y+6x^3y^2\\ 2,\\ a,=2xy\left(2x+3y-4\right)\\ b,=\left(x-3\right)\left(x+y\right)\\ c,=\left(x-2\right)\left(x+2\right)+y\left(x-2\right)=\left(x+y+2\right)\left(x-2\right)\\ d,=x^2-2x-5x+10=\left(x-2\right)\left(x-5\right)\\ 3,\\ a,\Leftrightarrow x^2-x^2+2x=2\\ \Leftrightarrow2x=2\Leftrightarrow x=1\\ b,\Leftrightarrow\left(x-2\right)\left(x-2+1\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Làm phép tính
a)x/x-2y+x/x+2y+4xy/4y2-x2
b)4x+7/2x+2-3x+6/2x+2
c)x+9/x2-9-3/x2+3x
d)1/x2+3x+2-1/x2-4
Câu 13: Đa thức x2 – 6x –4y2 + 9 được phân tích thành nhân tử có kết quả là
A. (x + 2y + 3)(x + 2y - 3)
B. (x – 3 – 2y)(x – 3 + 2y)
C. (x – 2y - 3)(x - 2y + 3)
D. (x – 3 – 4y)(x – 3 + 4y)
Cho hai đơn thức: M=-2x3y-xy+x2-6
N=3x3y-5x2-4xy+1
Tính M+N ; M-N
\(M+N=-2x^3y-xy+x^2-6+3x^3y-5x^2-4xy+1=x^3y-5xy-4x^2-5\)
\(M-N=-2x^3y-xy+x^2-6-3x^3y+5x^2+4xy-1=-5x^3y+3xy+6x^2-7\)
Đúng 1
Bình luận (0)





















