ac giúp e từ bài 5 vs ạ , e sắp phải nộp ròi

Những câu hỏi liên quan
Mọi người cứu e vs ạ!Huhuhuhu
\(\frac{x+2}{5}=\frac{3x-4}{-3}\)
E sắp phải nộp bài rồi
\(\frac{x+2}{5}=\frac{3x-4}{-3}\)
\(\Rightarrow\left(x+2\right).\left(-3\right)=\left(3x-4\right).5\)
\(\Rightarrow-3x-6=15x-20\)
Từ đây chuyển vế đổi dấu là xong nhé!
Đúng 0
Bình luận (0)
x+2/5=3x-4/-3
<=> (x+2).3=(3x-4).-3 (nhân chéo 2 vế)
<=> 3x+6=-9x+12
<=>12x=6
<=>x=6/12=1/2
vậy x=1/2
học tốt
Đúng 0
Bình luận (0)
xin lỗi mik nhân nhầm số nhưng bạn cứ thay vào rồi làm như thế là đc
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giúp e bài 8,9,11 vs ạ em đg cần gấp mai phải nộp r ạ
a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=8-3a=8-3\cdot7=-13\end{matrix}\right.\)
Đúng 0
Bình luận (0)
giúp e với e sắp phải nộp rùi ạ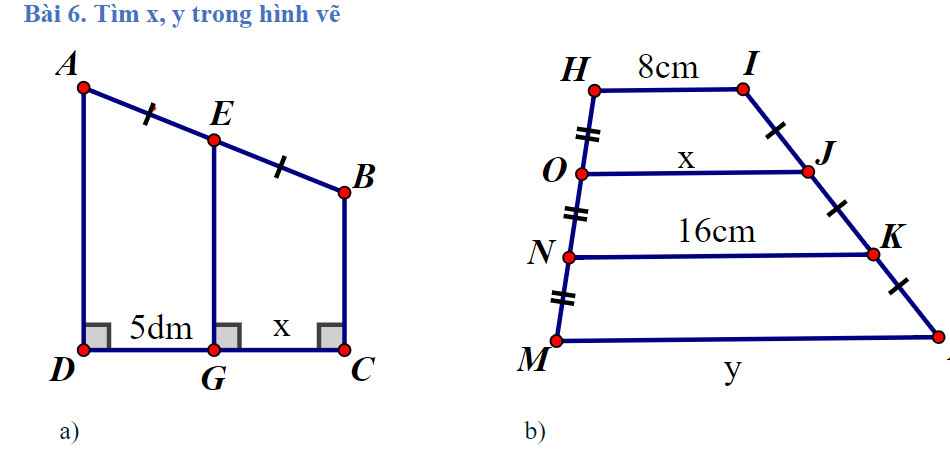
a) ta có AD vg góc DC
BC vg góc DC
EG vg góc DC
=> AD//BC//EG
Xét tg ABCD có AD//BC=> ABCD là hình thang
Xét hình thang ABCD có EG //BC//AD
AE= EB (gt)
=> G là td DC (EG là dg tb hthang ABCD)
=> DG=GC=5cm=> X =5 cm
b) Thêm dk là HI//OJ//NK//M...
Xét tg HINK có HI//NK(gt) => HINK là hthang
Xét Hthang HINK có OH =ON (gt)
IJ=IK(gt)
=>OJ là dg tb hình thang HINK
=> OJ= (HI+NK):2=(8+16):2=12 cm=> x=12 cm
Xét tg OJM... có OJ//M.. => OJM.. là hình thang
(cmt tương tự như ở trên)
=> M..= NK.2-OJ=16.2-12=20 cm
Bạn xem lại chỗ .... là gì nhé!
Đúng 0
Bình luận (0)
 giúp e 2 câu này với ạ e sắp phải nộp rùi ạ
giúp e 2 câu này với ạ e sắp phải nộp rùi ạ
a, văng vẳng, quang quác quác, tè te te
Tác dụng: Cho thấy sự huyên náo của các loài vật trong rừng núi, nó làm bức tranh thiên nhiên trở nên sinh động và đẹp hơn
b, đùng đùng, vù vù, lộp độp
Tác dụng: Cho thấy những dấu hiệu trước cơn mưa, cơn mưa diễn ra nhanh chóng và mạnh
Đúng 2
Bình luận (0)
Giúp e với ah, 23h56 phút là e phải nộp ròi ah
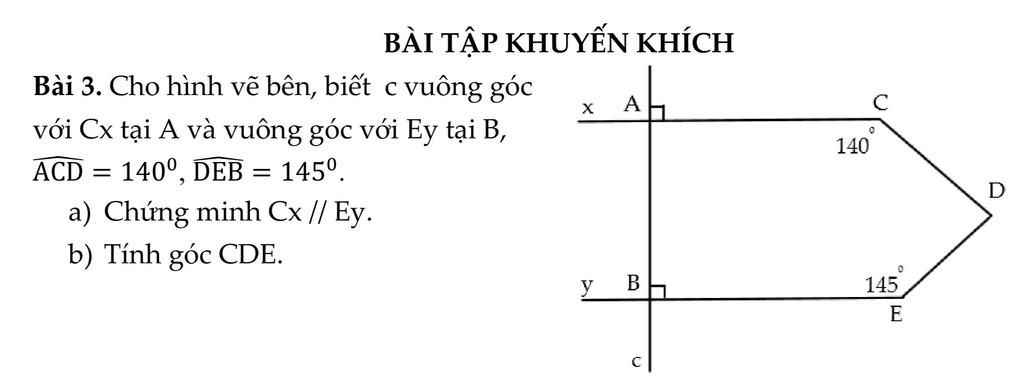
Mọi ngừi giúp e dzới, 22h là e phải nộp ròi ah ![]()
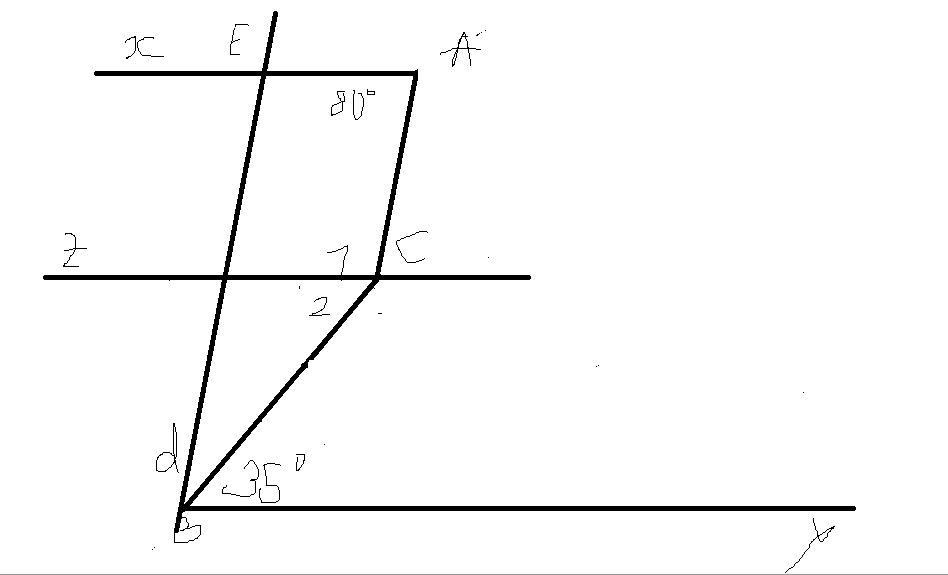
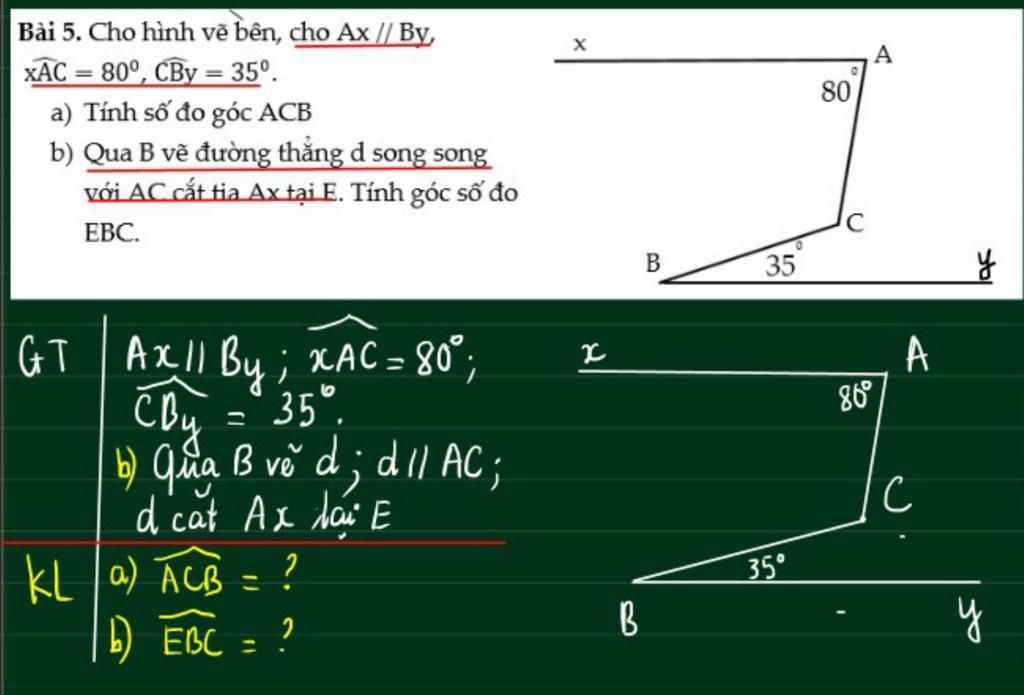
a, Giả sử: Cz // Ax // By
Do Cz // Ax \(\Rightarrow\widehat{A}+\widehat{C_1}=180^o\)(2 góc TCP)
\(\Rightarrow80^o+\widehat{C_1}=180^o\)
\(\Rightarrow\widehat{C_1}=180^o-80^o=100^o\)
Do Cz // By \(\Rightarrow\widehat{C_2}=\widehat{B}=35^o\)(2 góc so le trong)
Ta thấy: \(\widehat{ACB}=\widehat{C_1}+\widehat{C_2}=100^o+35^o=135^o\)
b, Do d // AC \(\Rightarrow\widehat{ACB}+\widehat{EBC}=180^o\)(2 góc TCP)
\(\Rightarrow135^o+\widehat{EBC}=180^o\)
\(\Rightarrow\widehat{EBC}=180^o-135^o=45^o\)
Đúng 1
Bình luận (1)
GIÚP EM BÀI 1,2,3,4, VỚI Ạ,4H CHIỀU PHẢI NỘP RÒI Ạ
GIÚP EM BÀI 1,2,3,4, VỚI Ạ,4H CHIỀU PHẢI NỘP RÒI Ạ
Bài 1:
c) \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - \sqrt{8-2\sqrt{7}} + \sqrt{2} \)
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - \sqrt{(\sqrt{7})^2 - 2\sqrt{7}+1} + \sqrt{2} \)
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - \sqrt{(\sqrt{7}-1)^2} + \sqrt{2} \)do
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - |\sqrt{7}-1| + \sqrt{2} \)
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - \sqrt{7}+1 + \sqrt{2} \) (do \(\sqrt{7} > 1 \))
⇔ \(C=\dfrac{5}{\sqrt{7}+\sqrt{2}} - (\sqrt{7} - \sqrt{2}) +1 \)
⇔ \(C=\dfrac{5-(\sqrt{7} - \sqrt{2})(\sqrt{7}+\sqrt{2})}{\sqrt{7}+\sqrt{2}} +1 \)
⇔ \(C=\dfrac{5-7+2}{\sqrt{7}+\sqrt{2}} +1 =\dfrac{0}{\sqrt{7}+\sqrt{2}} +1 \)
⇔ \(C = 0 + 1 = 1\)
Vậy \(C=1\)
Đúng 0
Bình luận (0)
Bài 3:
c) Ta có: \(M=\dfrac{Q}{P} \)
⇔ \(M=\dfrac{\dfrac{\sqrt{x}}{\sqrt{x}-2}}{\dfrac{\sqrt{x}+5}{\sqrt{x}-2} } \)
⇔ \(M=\dfrac{\sqrt{x}}{\sqrt{x}+5} \)
Mà: \(M<\dfrac{1}{2} \) ⇔ \(\dfrac{\sqrt{x}}{\sqrt{x}+5} <\dfrac{1}{2} \)
⇒ \(2\sqrt{x} < \sqrt{x}+5 \) (nhân 2 vế với \(2.(\sqrt{x} +5) >0\))
⇔ \(\sqrt{x}<5 \) ⇔ \(x<25\)
Kết hợp điều kiện ban đầu, ta đc:
Vậy khi \(0≤x<25\) và \(x≠4\) thì \(M=\dfrac{Q}{P} < \dfrac{1}{2} \)
Đúng 0
Bình luận (0)
Bài 3:
d) \(M= \dfrac{\sqrt{x}}{\sqrt{x}+5} \)
⇔ \(M= \dfrac{\sqrt{x}+5-5}{\sqrt{x}+5}=M= 1-\dfrac{5}{\sqrt{x}+5} \)
M đạt giá trị nguyên khi: \(x∈Z \) và \(\dfrac{5}{\sqrt{x}+5} ∈Z \)
\(\dfrac{5}{\sqrt{x}+5} ∈Z \) khi \((\sqrt{x}+5) ∈ Ư_{5}\)
Mà \(\sqrt{x}+5>0\) nên ta có bảng sau:
| \(\sqrt{x}+5\) | 1 | 5 |
| \(x\) | Loại | 0 (TM) |
Vậy \(x=0\) thì \(M\) nhận giá trị nguyên
Đúng 0
Bình luận (0)
giúp e mấy bài này vs ạ, lát nx e phải nộp r