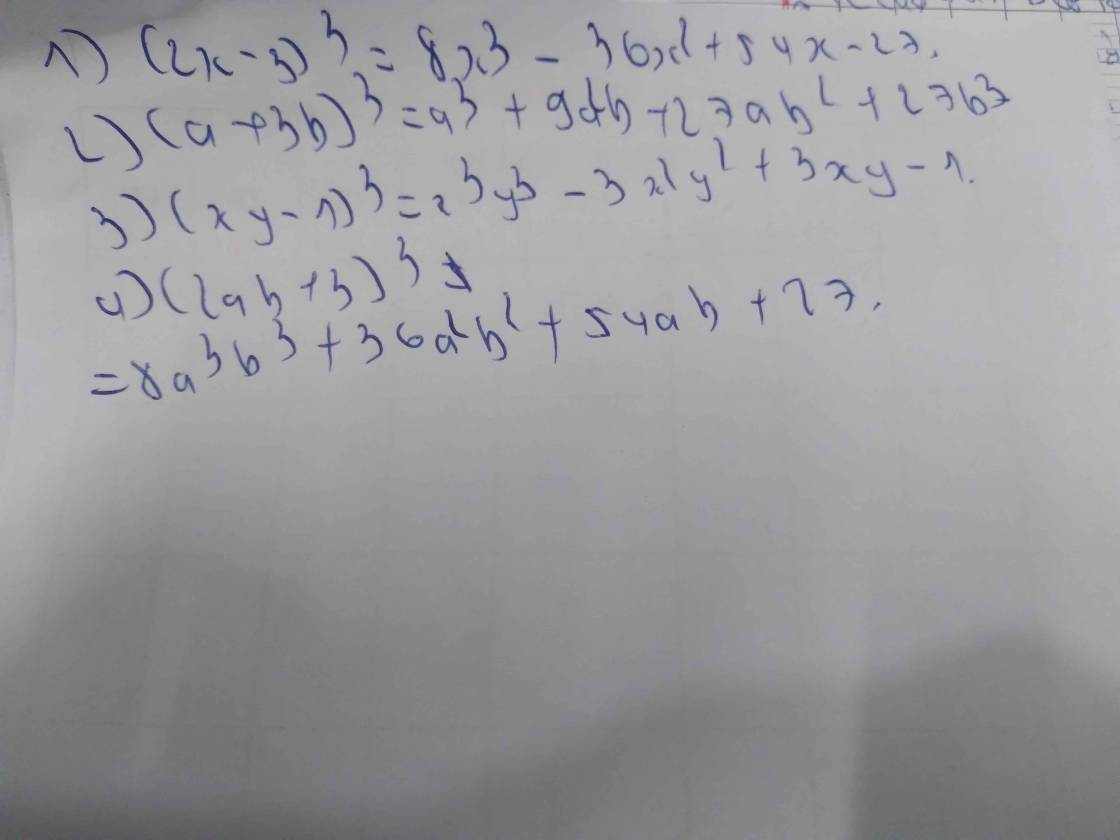BT9: viết các biểu thức sau thành đa thức 1, (a-1)(a+1)(a^2+1) 2, (xy+1)^2-(xy-1)^2

Những câu hỏi liên quan
Viết các biểu thức sau thành đa thức:
a) \(\left( {a - 1} \right)\left( {a + 1} \right)\left( {{a^2} + 1} \right)\) b) \({\left( {xy + 1} \right)^2} - {\left( {xy - 1} \right)^2}\)
`a, (a-1)(a+1)(a^2+1)`
`= (a^2-1)(a^2+1)`
`= a^4-1`
`b, (xy+1)^2 - (xy-1)^2`
`= x^2y^2 + 2xy + 1 - x^2y^2 + 2xy - 1`
`= 4xy`
Đúng 1
Bình luận (0)
a) \(\left(a-1\right)\left(a+1\right)\left(a^2+1\right)\)
\(=\left(a^2-1\right)\left(a^2+1\right)\)
\(=a^4-1\)
b) \(\left(xy+1\right)^2-\left(xy-1\right)^2\)
\(=\left[\left(xy+1\right)-\left(xy-1\right)\right]\left[\left(xy+1\right)+\left(xy-1\right)\right]\)
\(=\left(xy+1-xy+1\right)\left(xy+1+xy-1\right)\)
\(=4xy\)
Đúng 0
Bình luận (0)
BT7: viết các biểu thức sau thành đa thức 1, (2x-3)^3 2, (a+3b)^3 3, (xy-1)^3 4, (2ab+3)^3
Câu 1: Đa thức -2x^2y +xy + 1 đc viết thành tổng của 2 đa thức nào. Câu 2 : Đa thức x^2y^2 + 2xy -3 đc viết thành tổng của 2 đa thức nào. Câu 3 : Đa thức -2x^2y + xy +1 đc viết thành hiệu của 2 đa thức nào.Câu 4 : Đa thức x^2y^2 -2xy +3 đc viết thành hiệu của 2 đa thức nào.
Đọc tiếp
Câu 1: Đa thức -2x^2y +xy + 1 đc viết thành tổng của 2 đa thức nào.
Câu 2 : Đa thức x^2y^2 + 2xy -3 đc viết thành tổng của 2 đa thức nào.
Câu 3 : Đa thức -2x^2y + xy +1 đc viết thành hiệu của 2 đa thức nào.
Câu 4 : Đa thức x^2y^2 -2xy +3 đc viết thành hiệu của 2 đa thức nào.
Câu 1:
-2x²y + xy + 1 = -2x²y + (xy + 1)
Vậy -2x²y + xy + 1 được viết thành tổng của hai đa thức: -2x²y và xy + 1
Câu 2:
x²y² + 2xy - 3 = x²y² + (2xy - 3)
Vậy x²y² + 2xy - 3 được viết thành tổng của hai đa thức: x²y² và 2xy - 3
Câu 3:
-2x²y + xy + 1 = (xy + 1) - 2x²y
Vậy -2x²y + xy + 1 được viết thành hiệu của hai đa thức: xy + 1 và 2x²y
Câu 4:
x²y² - 2xy + 3 = (x²y² + 3) - 2xy
Vậy x²y² - 2xy + 3 được viết thành hiệu của hai đa thức: x²y² + 3 và 2xy
Đúng 3
Bình luận (1)
Hảy viết đa thức sau dưới đây thành tổng các đơn thức :
(a + 1) (xy + 1) + xy (x + y) + 1 - a (a là hằng số)
Bài 1 : Phân tích các đa thức sau thành nhân tử :1) 15x + 15y 2) 8x - 12y3) xy - x 4) 4x^2- 6xBài 2 : Phân tích các đa thức sau thành nhân tử :1) 2(x + y) - 5a(x + y) 2) a^2(x - 5) - 3(x - 5)3) 4x(a - b) + 6xy(a - b) 4) 3x(x - 1) + 5(x -1)Bài 3 : Tính giá trị của biểu thức :1) A 13.87 + 13.12 + 132) B (x - 3).2x + (x - 3).y tại x 13 và y 4Bài 4 : Tìm x :1) x(x - 5) - 2(x - 5) 0 2) 3x(x - 4) - x + 4 03) x(x - 7) -...
Đọc tiếp
Bài 1 : Phân tích các đa thức sau thành nhân tử :
1) 15x + 15y 2) 8x - 12y
3) xy - x 4) 4x^2- 6x
Bài 2 : Phân tích các đa thức sau thành nhân tử :
1) 2(x + y) - 5a(x + y) 2) a^2(x - 5) - 3(x - 5)
3) 4x(a - b) + 6xy(a - b) 4) 3x(x - 1) + 5(x -1)
Bài 3 : Tính giá trị của biểu thức :
1) A = 13.87 + 13.12 + 13
2) B = (x - 3).2x + (x - 3).y tại x = 13 và y = 4
Bài 4 : Tìm x :
1) x(x - 5) - 2(x - 5) = 0 2) 3x(x - 4) - x + 4 = 0
3) x(x - 7) - 2(7 - x) = 0 4) 2x(2x + 3) - 2x - 3 = 0
\(1,\\ 1,=15\left(x+y\right)\\ 2,=4\left(2x-3y\right)\\ 3,=x\left(y-1\right)\\ 4,=2x\left(2x-3\right)\\ 2,\\ 1,=\left(x+y\right)\left(2-5a\right)\\ 2,=\left(x-5\right)\left(a^2-3\right)\\ 3,=\left(a-b\right)\left(4x+6xy\right)=2x\left(2+3y\right)\left(a-b\right)\\ 4,=\left(x-1\right)\left(3x+5\right)\\ 3,\\ A=13\left(87+12+1\right)=13\cdot100=1300\\ B=\left(x-3\right)\left(2x+y\right)=\left(13-3\right)\left(26+4\right)=10\cdot30=300\\ 4,\\ 1,\Rightarrow\left(x-5\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ 2,\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ 3,\Rightarrow\left(3x-1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\end{matrix}\right.\\ 4,\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Đúng 4
Bình luận (0)
1. Tính Giá trị nhỏ nhất của biểu thứ (x+1)(x+2)(x+3)(x+6)+2010
2. Phân tích đa thức thành nhân tử (x-2)(x-4)(x-6)(x-8) +15
3. Tính giá trị biểu thức sau: x^2 +y= y^2 +x. tính giá trị của biểu thức sau A= (x^2 +y^2 +xy) : (xy-1)
bbgfhfygfdsdty64562gdfhgvfhgfhhhhh
\hvhhhggybhbghhguyg
Chỉ ra các đơn thức, đa thức trong các biểu thức sau:
\( - 3\); \(2z\); \(\dfrac{1}{3}xy + 1\); \( - 10{x^2}yz\); \(\dfrac{4}{{xy}}\); \(5x - \dfrac{z}{2}\); \(1 + \dfrac{1}{y}\)
Các đơn thức là:
\(-3;2z;-10x^2yz;\dfrac{4}{xy}\)
Các đa thức là:
\(\dfrac{1}{3}xy+1;5x-\dfrac{z}{2};1+\dfrac{1}{y}\)
Đúng 1
Bình luận (0)
Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức?A. 3x2yz B. 2x +3y3 C. 4x2 - 2x D. xy – 7Câu 2. Trong các đa thức sau, đa thức nào là đa thức nhiều biến?A. 3x3 – 7xy B. 5y3 – 2y C. -3z2 D. 2x – 3Câu 3. Đa thức 3x3y+x5 + 6 có bậc là:A. 6 B. 5 C. 3 D. 2Câu 4: Đơn thức nào đồng dạng vớ...
Đọc tiếp
Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức?
A. 3x2yz B. 2x +3y3 C. 4x2 - 2x D. xy – 7
Câu 2. Trong các đa thức sau, đa thức nào là đa thức nhiều biến?
A. 3x3 – 7xy B. 5y3 – 2y C. -3z2 D. 2x – 3
Câu 3. Đa thức 3x3y+x5 + 6 có bậc là:
A. 6 B. 5 C. 3 D. 2
Câu 4: Đơn thức nào đồng dạng với đơn thức 2x3y?
A. 2xy B. -5xy3 C. x3y D. 2x3y3
Câu 5: Với a, b là hai số bất kì, trong các đẳng thức sau, đẳng thức nào không phải hằng đẳng thức?
A. (a+b)2 =a2 +2ab+b2 B. a2 – 1 =3a C. a(2a+b) =2a2 + ab D. a(b+c) =ab+ac
Câu 6: Biểu thức ![]() bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
A. | B. | C. | D. |
Câu 7: Tứ giác lồi ABCD có  ,
,  ,
,  Số đo góc B là
Số đo góc B là
A. 1100 B. 3600 C. 1800 D. 1000
Câu 8: Hình thang có hai đường chéo bằng nhau là
A. Hình thang cân. | B. Hình thoi. | C. Hình bình hành. | D.Hình thang vuông. |
Câu 9: Tứ giác có các cạnh đối bằng nhau là
A. hình thoi. | B. hình bình hành. |
C. hình chữ nhật. | D. hình thang cân. |
Câu 10: Hình bình hành có một góc vuông là
A. hình thoi. | B. hình thang vuông. |
C. hình chữ nhật. | D. hình vuông. |
Câu 11: Hình bình hành có hai cạnh kề bằng nhau là
A. hình thang cân. | B. hình thang. |
C. hình chữ nhật. | D. hình thoi. |
II. Tự luận.
Bài 1: Thực hiện phép tính:
a) 2x.(x2 – 3x +5) b) ![]()
c) (x -3) (2x +1) d) 
![]()
Bài 2: Phân tích đa thức thành nhân tử:
a) 3x2 - 9xy b) ![]() c) x2 – 4x + 4 – y2
c) x2 – 4x + 4 – y2
Bài 2:
a: \(3x^2-9xy\)
\(=3x\cdot x-3x\cdot3y\)
=3x(x-3y)
c: \(x^2-4x+4-y^2\)
\(=\left(x^2-4x+4\right)-y^2\)
\(=\left(x-2\right)^2-y^2\)
\(=\left(x-2-y\right)\left(x-2+y\right)\)
Bài 1:
a: \(2x\left(x^2-3x+5\right)\)
\(=2x\cdot x^2-2x\cdot3x+2x\cdot5\)
\(=2x^3-6x^2+10x\)
c: (x-3)(2x+1)
\(=2x^2+x-6x-3\)
\(=2x^2-5x-3\)
I: Trắc nghiệm
Câu 1: A
Câu 2: A
Câu 3: B
Câu 4: C
Câu 5: B
Câu 8: A
Câu 9: B
Câu 10: C
Câu 11: D
Đúng 3
Bình luận (0)
Bài 1: Phân tích đa thức sau thànBài 1: Phân tích đa thức sau thành nhân tử a) x 2 – xy + x – y b) x 2 + 5x + 6 c) 2xy - x 2 - y 2 +16h nhân tử a) x 2 – xy + x – y b) x 2 + 5x + 6 c) 2xy - x 2 - y 2 +16
a) \(x^2-xy+x-y\)
\(=x\left(x-y\right)+\left(x-y\right)\)
\(=\left(x+1\right)\left(x-y\right)\)
b) \(x^2+5x+6\)
\(=x^2+2x+3x+6\)
\(=x\left(x+2\right)+3\left(x+2\right)\)
\(=\left(x+3\right)\left(x+2\right)\)
\(2xy-x^2-y^2+16\)
\(=16-\left(x-y\right)^2\)
\(=\left(4-x+y\right)\left(4+x-y\right)\)
Xem thêm câu trả lời