tim bcn
bcn (3;4)
bcn (10;15;30)
bcn (9;10 )
bcn (12;16;48)
giup minh voi dang can gap mai di hoc roi chua lam xong giup voi
minh tha cho 2 tich cho ban nhanh
Chứng minh D Ax ^ = B C N ^ theo nhiều cách
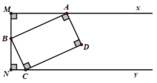
Cho góc nhọn zOy.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Trên tia Ax lấy điểm của AC và BD.
a,Chứng minh: ADN=BCN từ đó suy ra OAC = OBD?
b,Gọi N là giao điểm của AC và BD.Chứng minh tam giác ADN = BCN và ON là tia phân giác của góc xOy
c,Gọi H,K lần lượt là giao điểm của ON với DC và AB.Chứng minh OH vuông góc CD,AB // CD.
Trên tia Ax lấy điểm gì vậy bạn?
Cho góc nhọn zOy.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Trên tia Ax lấy điểm của AC và BD.
a,Chứng minh: góc ADN=BCN từ đó suy ra tam giác OAC = OBD?
b,Gọi N là giao điểm của AC và BD.Chứng minh tam giác ADN = BCN và ON là tia phân giác của góc xOy
c,Gọi H,K lần lượt là giao điểm của ON với DC và AB.Chứng minh OH vuông góc CD,AB // CD.
Cho tam giác ABC vuông tại C, đường cao CN. Phân giác g(NCA) và g(BCN) cắt AB lần lượt tại K
và L. Gọi T và S lần lượt là giao các đường phân giác trong của tam giác BCN và NCA.
a) Đường thẳng AS cắt CT tại E. Chứng minh tam giác CAE vuông.
b) Chứng minh rằng g(TKS) = g(TLS).
ai chơi freefire thì kb với mình
Cho tam giác ABC có bằng 210 cm2 . Trên AC lấy điểm N sao cho AN = 2/ 3 NC. Tính diện tích tam giác ABN và diện tích tam giác BCN.
Lời giải:
Ta thấy:
$S_{ABN}+S_{BCN}=S_{ABC}=210$ (cm2)
$\frac{S_{ABN}}{S_{BCN}}=\frac{AN}{CN}=\frac{2}{3}$
Tổng số phần bằng nhau: $2+3=5$ (phần)
Diện tích $ABN$ là: $210:5\times 2=84$ (cm2)
Diện tích $BCN$: $210-84=126$ (cm2)
Cho 3 điểm A(-2;4), B(1;-3), C(2;1)
a) Tìm N sao cho A là trọng tâm của tam giác BCN
Vì A trọng tâm tam giác BCN
\(\Rightarrow x_A=\frac{x_N+x_B+x_C}{3}\Leftrightarrow-2=\frac{x_N+1+2}{3}\)
\(\Rightarrow x_N=-9\)
\(y_A=\frac{y_N+y_B+y_C}{3}\Leftrightarrow4=\frac{y_N-3+1}{3}\)
\(\Rightarrow y_N=14\)
\(\Rightarrow N\left(-9;14\right)\)
Cho tam giác ABC bất kì.Về phía ngoài tam giác ABC dựng các tam giác ABM,BCN,CAP,ABD sao cho \(\widehat{CAP}=\widehat{CBN}=45^o;\widehat{ACP}=\widehat{BCN}=30^o;\widehat{ABM}=\widehat{BAM}=15^o,\Delta ABD\)đều .CMR \(\Delta\)MNP vuông cân
cho tam giác ABC. trên AC lấy điểm N sao cho AN = 2/3 NC. biết diện tích tam giác ABC bằng 180cm2. tính diện tích tam giác ABN và diện tích tam giác BCN
Kẻ BK vuông góc với AC
\(S_{ABN}=\dfrac{1}{2}\cdot BK\cdot AN\)
\(S_{ACB}=\dfrac{1}{2}\cdot BK\cdot AC\)
=>\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{AN}{AC}=\dfrac{2}{5}\)
=>\(S_{ABN}=72\left(cm^2\right)\)
=>\(S_{BCN}=108\left(cm^2\right)\)
cho tam giac abc tren canh ab lay diem n sao cho bn=2/3 ab tren canh aclay diem m saocho cm=2/3ac chung to rang dt bmc=dt bcn va =2/3 dttg abc
SBMC = \(\frac{2}{3}\) SABC ( vì 2 tam giác có chung chiều cao hạ từ B xuống AC và CM=2/3 AC)
SBCN=2/3 SABC ( vì 2 tam giác có chung chiều cao hạ từ C xuống AB và BN=2/3 AB)
=> SBMC=SBCN ( vì cùng bằng 2/3 SABC)