sắp xếp tsl giác cos37 độ; sin37 độ; cos25 độ; sin 25 độ theo thứ tự tăng dần.

Những câu hỏi liên quan
sắp xếp các tỉ số lượng giác sau theo thứ tự bé đến lớn:
a) sin35, cos28, sin34 72',cos62 ,sin 45
a) cos37, cos56 30', sin 72, cos59, sin47
a: cos28=sin62
cos62=sin28
28 độ<35 độ<34 độ72p<45 độ<62 độ
=>sin 28<sin35<sin34 độ72p<sin45<sin62
=>cos62<sin35p<sin34 độ 72p<sin45<cos28
b:sin 72=cos18
sin47=cos43
Vì 18<37<43<56 độ30'<59
nên cos 18>cos37>cos43>cos56 độ30'>cos59
=>sin72>cos37>sin47>cos56 độ30'>cos 59
Đúng 0
Bình luận (0)
\(a)Ta\) \(có:\)
\(cos28=sin62\\ cos62=sin28\)(2 góc phụ nhau)
\(sin34,72'=sin35,3\)
\(sin28< sin35< sin35,2< sin45< sin62\\ \Rightarrow cos62< sin35< sin34,72'< sin45< cos28\)
a') Ta có:
\(sin72=cos18\\ sin47=cos43\)(2 góc phụ nhau)
\(cos56\) \(30'=cos56,5\)
\(cos59< cos56,5< cos43< cos37< cos18\\ \Rightarrow cos59< cos56,30'< sin47< cos37< sin72\)
Đúng 0
Bình luận (0)
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR trong Hình 3a.
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC trong Hình 3b.
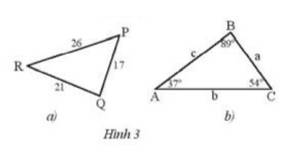
a) Ta có độ dài các cạnh tam giác PQR theo thứ tự từ nhỏ đến lớn là PQ, QR, RP
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ra có các góc tam giác PQR theo thứ tự từ nhỏ đến lớn là R, P, Q
b) Ta có số đo các góc theo tứ tự từ nhỏ đến lớn của tam giác ABC là A, C, B
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ta có các cạnh tam giác ABC theo thứ tự từ nhỏ đến lớn là a, c, b.
Đúng 0
Bình luận (0)
Cho tam giác ABC trong Hình 1.
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a,b,c
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc A,B,C là các góc đối diện với ba cạnh a,b,c.
- Nêu nhận xét của em về hai kết quả sắp xếp trên.
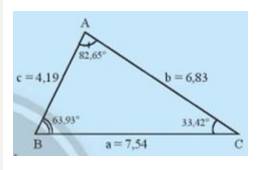
- Độ dài các cạnh từ nhỏ đến lớn là c, b, a
- Các góc từ nhỏ đến lớn là C, B, A
- Ta thấy trong tam giác ABC cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.
Đúng 0
Bình luận (0)
sắp xếp các tỉ số lượng giác theo thứ tự tăng dần:
sin 49 độ, cot 15 độ, tan 65 độ, cos 50 độ, cot 41 độ
Cho tam giác ABC có goc A = 60 độ, B = 50 độ hãy sắp xếp Các cạnh có độ dài từ bé đến lớn
Vì tổng ba góc trong 1 tam giác bằng 1800
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
hay 600 + 500 + \(\widehat{C}=180^0\)
=> \(\widehat{C}=180^0-110^0=70^0\)
Ta có : \(\widehat{C}>\widehat{A}>\widehat{B}\left(70^0>60^0>50^0\right)\)
\(\Leftrightarrow AB>BC>AC\)
hay AC < BC < AB
Đúng 0
Bình luận (0)
độ dài góc C là
180-50-60=70
vì góc A đối diện với cạnh BC
góc B đối diện với cạnh AC
góc C đối diện với cạnh AB
ma goc C>A>B =>AB>BC>AC=>AC<BC<AB
mk nah bn
Đúng 0
Bình luận (0)
không dùng bảng số và máy tính, sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần:
tg 32 độ; cotg 61 độ; cotg 18 độ; tg 50 độ; cotg 90 độ
\(\cot90^0=\tan0^0< \cot61^0=\tan29^0< \tan32^0< \tan50^0< \tan72^0=\cot18^0\)
Đúng 0
Bình luận (0)
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần
sin 47 độ, cos 23 độ, sin 16 độ, cos 46 độ
Mik chỉ bt làm thế này thôi bạn áp dụng vào bài nhá
cos75 = sin(90-75) = sin15
cos18 = sin(90-18) = sin72
Vì 15 < 65 < 70 < 72 < 79
Nên sin15 < sin 65 < sin70 < sin72 < sin79
Tít cho mik
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần(giải thích vì sao): Sin78 độ ; có24độ35’ ; sin40độ ; cos87độ20’ ; sin42độ .
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần(giải thích vì sao): Sin78 độ ; có24độ35’ ; sin40độ ; cos87độ20’ ; sin42độ .
\(\cos87^020'=\sin2^040'< \sin40^0< \sin42^0< \sin65^025'=\cos24^035'< \sin78^0\)
Đúng 2
Bình luận (0)

















