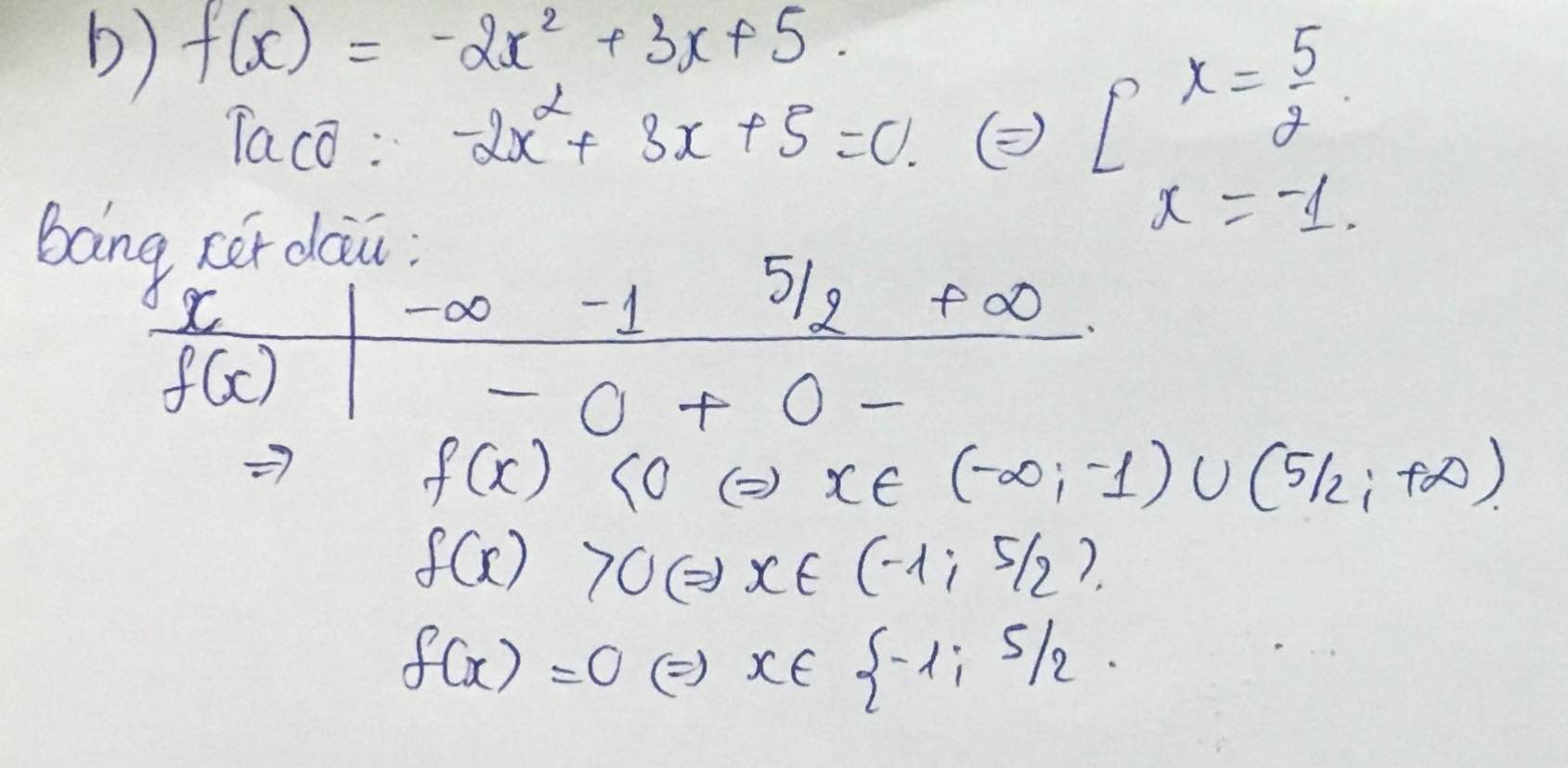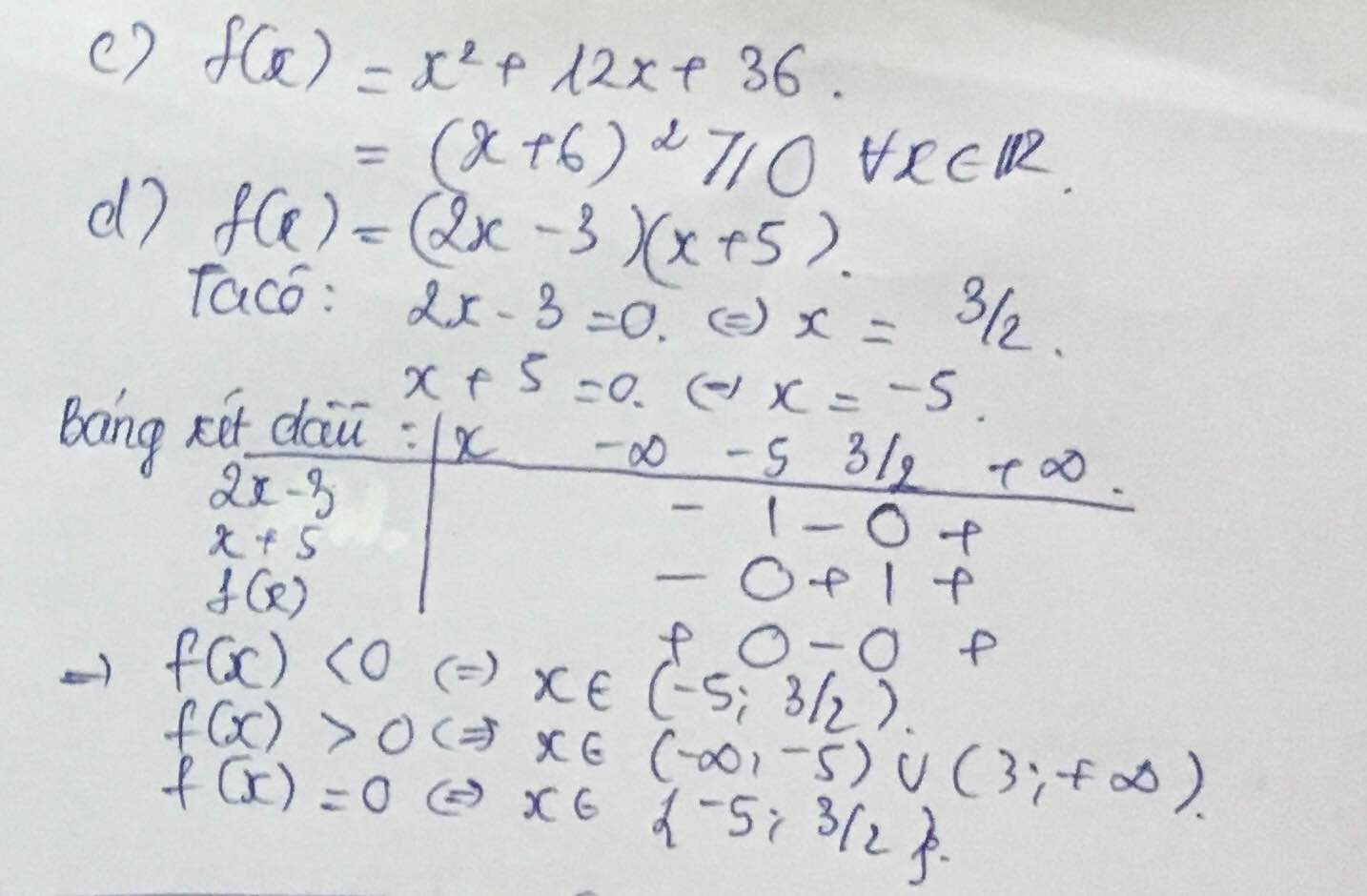\(\left|2x+1\right|=\left|12x-5\right|\)

Những câu hỏi liên quan
Rút gọn các phân thức:
a)\(\dfrac{14xy^5\left(2x-3y\right)}{21x^2y\left(2x-3y\right)^2}\) b)\(\dfrac{8xy\left(3x-1\right)^3}{12x^3\left(1-3x\right)}\)
c) \(\dfrac{20x^2-45
}{\left(2x+3\right)^2}\) d) \(\dfrac{5x^2-10xy}{2\left(2y-x\right)^3}\)
\(a,=\dfrac{2y^4}{3x\left(2x-3y\right)}\\ b,=-\dfrac{2y\left(3x-1\right)^2}{3x^2}\\ c,=\dfrac{5\left(4x^2-9\right)}{\left(2x+3\right)^2}=\dfrac{5\left(2x-3\right)\left(2x+3\right)}{\left(2x+3\right)^2}=\dfrac{5\left(2x-3\right)}{2x+3}\\ d,=\dfrac{5x\left(x-2y\right)}{-2\left(x-2y\right)^3}=-\dfrac{5x}{2\left(x-2y\right)^2}\)
Đúng 5
Bình luận (0)
b) \(f\left(x\right)=-2x^2+3x+5\)
c) \(f\left(x\right)=x^2+12x+36\)
d) \(f\left(x\right)=\left(2x-3\right).\left(x+5\right)\)
A.tính
\(25x^2-10x+1\)
B.rút gọn
\(\left(x-2\right).\left(x^2+2x+4\right)-6x^2+12x\)
(2x+5) .(5-2x)+(x-5).(5+4x)
B: rút gọn
a) Ta có: \(\left(x-2\right)\left(x^2+2x+4\right)-6x^2+12x\)
\(=x^3-6x^2+12x-8\)
\(=\left(x-2\right)^3\)
b) Ta có: \(\left(2x+5\right)\left(5-2x\right)+\left(x-5\right)\left(4x+5\right)\)
\(=25-4x^2+4x^2+5x-20x-25\)
=-15x
Đúng 0
Bình luận (0)
Giaỉ các PT:
a) \(\left(x^2+1\right)^2=4\left(2x-1\right)\)
b) x(x+1)(x+2)(x+3)=24
c)\(\left(12x+7\right)^2\left(3x+2\right)\left(2x+1\right)=3\)
d)\(\left(x^2-9\right)^2=12x+1\)
e)\(\left(x-1\right)^5+\left(x+3\right)^5=242\left(x+1\right)\)
Giup mk vs mn
b) x(x+1)(x+2)(x+3)=24
(x2+3x)(x2+3x+2)=24 (1)
Đặt x2+3x+1=a
Khi đó(1)<=>(a-1)(a+1)=24
a2-1=24 <=>a2=25<=>a=5;-5
a=5=>x2+3x+1=5=>x2+3x-4=0=>(x-1)(x+4)=0=>x=1,-4
a=-5=>x^2+3x+1=-5=>x2+3x+6=0=>(x+\(\frac{3}{2}\))2+\(\frac{15}{4}\)=0
=>pt vô nghiệm
giải pt:
a,\(\left(13-4x\right)\sqrt{2x-3}+\left(4x-3\right)\sqrt{5-2x}=2+8\sqrt{-4x^2+16x-15}\)
b,\(\left(9x-2\right)\sqrt{3x-1}+\left(10-9x\right)\sqrt{3-3x}-4\sqrt{-9x^2+12x-3}=4\)
c, \(\left(6x-5\right)\sqrt{x+1}-\left(6x+2\right)\sqrt{x-1}+4\sqrt{x^2-1}=4x-3\)
giải pt :
a,\(\left(6x-5\right)\sqrt{x+1}-\left(6x+2\right)\sqrt{x-1}+4\sqrt{x^2-1}=4x-3\)
b, \(\left(9x-2\right)\sqrt{3x-1}+\left(10-9x\right)\sqrt{3-3x}-4\sqrt{-9x^2+12x-3}=4\)
c, \(\left(13-4x\right)\sqrt{2x-3}+\left(4x-3\right)\sqrt{5-2x}=2+8\sqrt{-4x^2+16x-15}\)
Giải phương trình:
\(\frac{\left(6x^4+4x^3-12x^2+9\right)\left(2x^3+7\right)-3\left(4x^3+5\right)\sqrt{6x^4+4x^3-12x^2+9}}{\sqrt{\left(6x^4+4x^3-12x^2+9\right)^3}-18x^3-9}=1\)
=))
giải hệ phương trình
\(\left\{{}\begin{matrix}8\left(x^3-1\right)+6xy^2=y\left(12x^2+y^2\right)\\\left(x^2+y-4x\right)\left(x^2-y^2-2x-5\right)=14\end{matrix}\right.\)
\(8x^3-12x^2y+6xy^2-y^3=8\)
\(\Leftrightarrow\left(2x-y\right)^3=8\)
\(\Leftrightarrow2x-y=2\)
\(\Rightarrow y=2x-2\)
Thế xuống pt dưới:
\(\left(x^2-2x-2\right)\left(-3x^2+6x-9\right)=14\)
Đặt \(x^2-2x=t\)
\(\Rightarrow\left(t-2\right)\left(-3t-9\right)=14\)
\(\Leftrightarrow...\)
Đúng 2
Bình luận (0)
Tìm x, biết:
a) \(\left(3x-1\right)^2-\left(2x+3\right)^2=0\)
b)\(\left(12x-5\right)\left(4x-1\right)+\left(3x-7\right)\left(1-16x\right)=81\)
Giải:
a) \(\left(3x-1\right)^2-\left(2x+3\right)^2=0\)
\(\Leftrightarrow\left(3x-1+2x+3\right)\left(3x-1-2x-3\right)=0\)
\(\Leftrightarrow\left(5x+2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{5}\\x=4\end{matrix}\right.\)
Vậy ...
b) \(\left(12x-5\right)\left(4x-1\right)+\left(3x-7\right)\left(1-16x\right)=81\)
\(\Leftrightarrow48x^2-20x-12x+5+3x-7-48x^2+112x=81\)
\(\Leftrightarrow83x-2=81\)
\(\Leftrightarrow83x=83\)
\(\Leftrightarrow x=1\)
Vậy ...
Đúng 0
Bình luận (0)