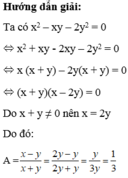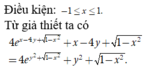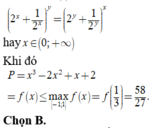Cho biểu thức
\(A=\frac{x-y}{x+y}\).Nếu x2-2y2=xy
Và y khác 0; x+y khác 0

Những câu hỏi liên quan
Tính giá trị biểu thức P= x-y/x+y . Biết x2 _ 2y2 = xy ( x+y khác 0 , y khác 0 )
Bạn tham khảo bài này nha
Link:https://olm.vn/hoi-dap/detail/266831819020.html
Chúc bạn học tốt
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
Đúng 1
Bình luận (0)
b) Tính giá trị biểu thức A = (x−y)(x2−xy)−x(x2+2y2) tại x=2;y=−3
\(A=\left(x-y\right)\left(x^2-xy\right)-x\left(x^2+2y^2\right)\)
\(=x^3-x^2y-x^2y+xy^2-x^3-2xy^2\)
\(=-2x^2y-xy^2\)
\(=-2\cdot2^2\cdot\left(-3\right)-2\cdot\left(-3\right)^2\)
\(=8\cdot3-2\cdot9\)
=6
Đúng 0
Bình luận (0)
Tính giá trị của phân thức A = x - y x + y biết x 2 - 2 y 2 = x y (y ≠ 0; x + y ≠ 0)
Bài 6
Ạ)Cho a2 +4b2+9c2=2ab+6bc+3ca. Tính giá trị của biểu thức
A=(a-2b+1)2022+(2b-3c-1)2023+(3c-a+1)2024
B) cho x,y thỏa mãn x2+2xy+6x+6y+2y2+8=0 tìm giá trị lớn nhất và nhỏ nhất của biểu thức A= x+y+2024
Bài 6
Ạ)Cho a2 +4b2+9c2=2ab+6bc+3ca. Tính giá trị của biểu thức
A=(a-2b+1)2022+(2b-3c-1)2023+(3c-a+1)2024
B) cho x,y thỏa mãn x2+2xy+6x+6y+2y2+8=0 tìm giá trị lớn nhất và nhỏ nhất của biểu thức A= x+y+2024
A.
$a^2+4b^2+9c^2=2ab+6bc+3ac$
$\Leftrightarrow a^2+4b^2+9c^2-2ab-6bc-3ac=0$
$\Leftrightarrow 2a^2+8b^2+18c^2-4ab-12bc-6ac=0$
$\Leftrightarrow (a^2+4b^2-4ab)+(a^2+9c^2-6ac)+(4b^2+9c^2-12bc)=0$
$\Leftrightarrow (a-2b)^2+(a-3c)^2+(2b-3c)^2=0$
$\Rightarrow a-2b=a-3c=2b-3c=0$
$\Rightarrow A=(0+1)^{2022}+(0-1)^{2023}+(0+1)^{2024}=1+(-1)+1=1$
Đúng 0
Bình luận (1)
B.
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+y^2+6x+6y+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+9+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$ (do $y^2\geq 0$ với mọi $y$)
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
$\Rightarrow A_{\min}=2020; A_{\max}=2022$
Đúng 1
Bình luận (0)
Ko thèm tick cho người ta mà đòi hỏi câu khác ✅
Đúng 0
Bình luận (0)
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y
Rút gọn các biểu thức sau:
a
)
y
x
x
2
y
4
v
ớ
i
x
0
;
y
≠
0
b
)
2
y
2
.
x
4...
Đọc tiếp
Rút gọn các biểu thức sau:
a ) y x x 2 y 4 v ớ i x > 0 ; y ≠ 0 b ) 2 y 2 . x 4 4 y 2 y < 0 c ) 5 x y 25 x 2 y 6 x < 0 ; y > 0 d ) 0 , 2 x 3 y 3 16 x 4 y 8 v ớ i x ≠ 0 ; y ≠ 0
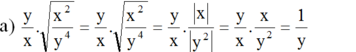
(Vì x > 0 nên |x| = x; y 2 > 0 với mọi y ≠ 0)
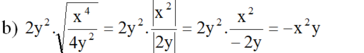
(Vì x 2 ≥ 0 với mọi x; và vì y < 0 nên |2y| = – 2y)
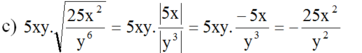
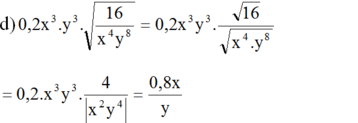
(Vì
x
2
y
4
=
(
x
y
2
)
2
>
0
với mọi x ≠ 0, y ≠ 0)
(Vì x < 0 nên |5x| = – 5x; y > 0 nên | y 3 | = y 3 )
Đúng 0
Bình luận (0)
Cho 2 hai số thực x, y thỏa mãn
e
x
-
4
y
+
1
-
x
2
-
e
y
2
+
1
-
x...
Đọc tiếp
Cho 2 hai số thực x, y thỏa mãn e x - 4 y + 1 - x 2 - e y 2 + 1 - x 2 - y = y 2 - x 4 . Giá trị lớn nhất của biểu thức P = x 3 + 2 y 2 - 2 x 2 + 8 y - x + 2 bằng
A. 2
B. 58 27
C. 115 27
D. 122 27