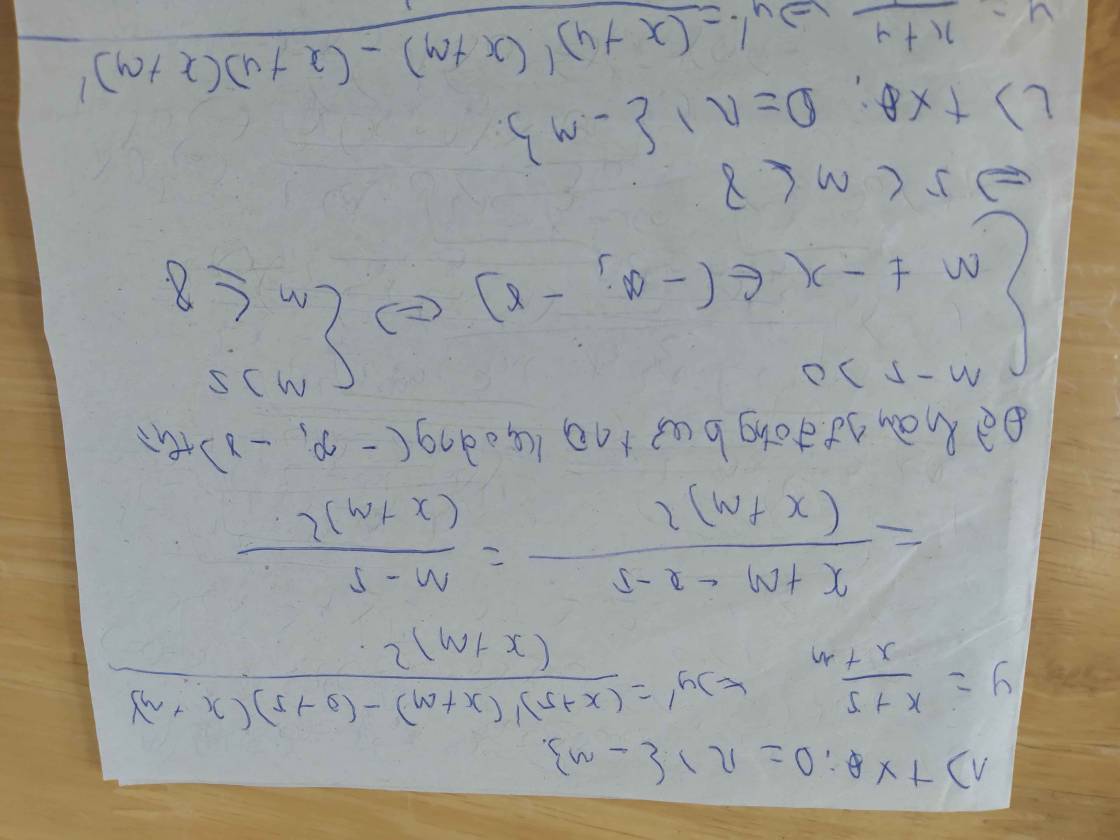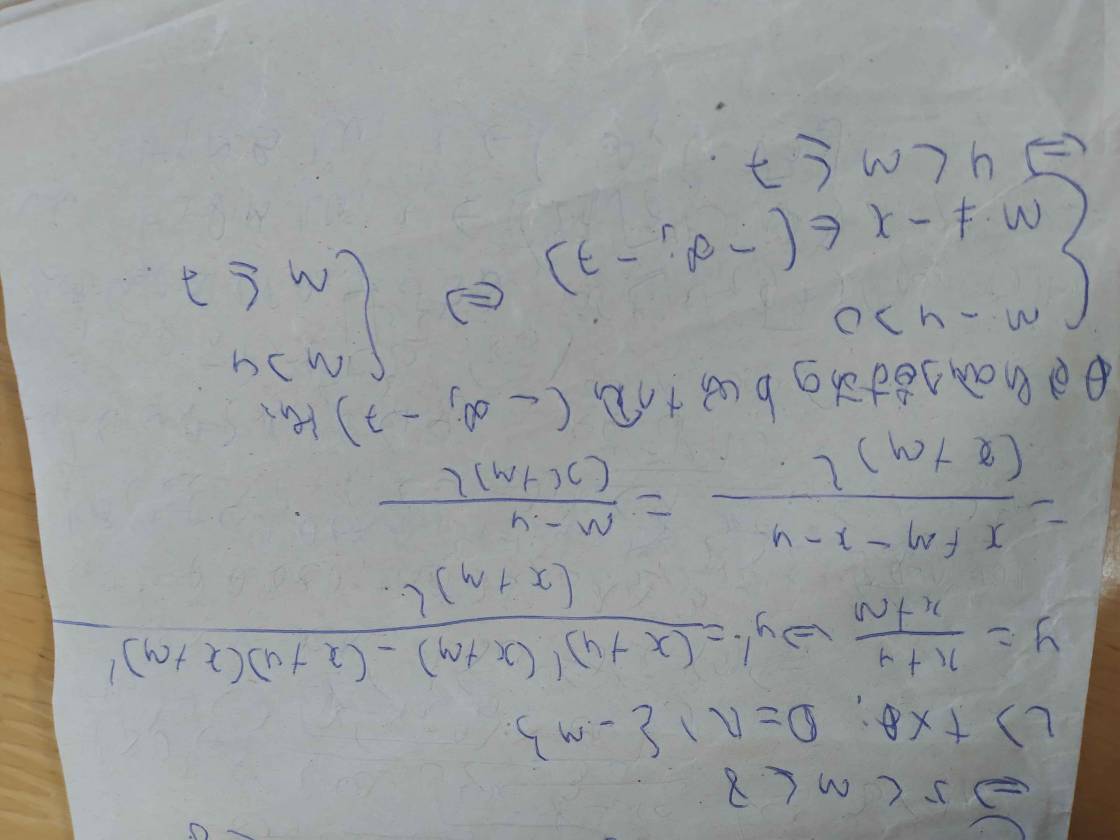Ta có: y′=x2−2(m+1)x+m2+2my′=x2−2(m+1)x+m2+2m

Để hàm số y=x33−(m+1)x2+(m2+2m)x+1y=x33−(m+1)x2+(m2+2m)x+1 nghịch biến trên $(2;3)$ thì ${}^{}<0$ với mọi x∈(2;3).x∈(2;3).

Tức là khoảng $(2;3)$ nằm trong khoảng hai nghiệm phương trình ${}^{}=0$ (Do y′=x2−2(m+1)x+m2+2my′=x2−2(m+1)x+m2+2m có hệ số của  dương).

{Δ′>0x1≤2<3≤x2⇔⎧⎪ ⎪⎨⎪ ⎪⎩(m+1)2−m2−2m>0(x1−2)(x2−2)≤0(x1−3)(x2−3)≤0⇔⎧⎪⎨⎪⎩1>0x1x2−2(x1+x2)+4≤0x1x2−3(x1+x2)+9≤0{Δ′>0x1≤2<3≤x2⇔{(m+1)2−m2−2m>0(x1−2)(x2−2)≤0(x1−3)(x2−3)≤0⇔{1>0x1x2−2(x1+x2)+4≤0x1x2−3(x1+x2)+9≤0

⇔{m2+2m−2.2.(m+1)+4≤0m2+2m−3.2.(m+1)+9≤0⇔{m2−2m≤0m2−4m+3≤0⇔{0≤m≤21≤m≤3⇔1≤m≤2

Ta có: y′=x2−2(m+1)x+m2+2my′=x2−2(m+1)x+m2+2m

Để hàm số y=x33−(m+1)x2+(m2+2m)x+1y=x33−(m+1)x2+(m2+2m)x+1 nghịch biến trên (2;3)(2;3) thì y′<0y′<0 với mọi x∈(2;3).x∈(2;3).

Tức là khoảng (2;3)(2;3) nằm trong khoảng hai nghiệm phương trình y′=0y′=0 (Do y′=x2−2(m+1)x+m2+2my′=x2−2(m+1)x+m2+2m có hệ số của x2x2 dương).

{Δ′>0x1≤2<3≤x2⇔⎧⎪ ⎪⎨⎪ ⎪⎩(m+1)2−m2−2m>0(x1−2)(x2−2)≤0(x1−3)(x2−3)≤0⇔⎧⎪⎨⎪⎩1>0x1x2−2(x1+x2)+4≤0x1x2−3(x1+x2)+9≤0{Δ′>0x1≤2<3≤x2⇔{(m+1)2−m2−2m>0(x1−2)(x2−2)≤0(x1−3)(x2−3)≤0⇔{1>0x1x2−2(x1+x2)+4≤0x1x2−3(x1+x2)+9≤0

⇔{m2+2m−2.2.(m+1)+4≤0m2+2m−3.2.(m+1)+9≤0⇔{m2−2m≤0m2−4m+3≤0⇔{0≤m≤21≤m≤3⇔1≤m≤2

ai làm có thưởng 2điem

1: TXĐ: D=R\{3}

\(y=\dfrac{x^2-6x+10}{x-3}\)

=>\(y'=\dfrac{\left(x^2-6x+10\right)'\left(x-3\right)-\left(x^2-6x+10\right)\left(x-3\right)'}{\left(x-3\right)^2}\)

=>\(y'=\dfrac{\left(2x-6\right)\left(x-3\right)-\left(x^2-6x+10\right)}{\left(x-3\right)^2}\)

=>\(y'=\dfrac{2x^2-12x+18-x^2+6x-10}{\left(x-3\right)^2}\)

=>\(y'=\dfrac{x^2-6x+8}{\left(x-3\right)^2}\)

Đặt y'<=0

=>\(\dfrac{x^2-6x+8}{\left(x-3\right)^2}< =0\)

=>\(x^2-6x+8< =0\)

=>(x-2)(x-4)<=0

=>2<=x<=4

Vậy: Khoảng đồng biến là [2;3) và (3;4]

Bài 1: 

a: Để hàm số đồng biến khi x>0 thì m-1>0

hay m>1

b: Để hàm số nghịch biến khi x>0 thì 3-m<0

=>m>3

c: Để hàm số nghịch biến khi x>0 thì m(m-1)<0

hay 0<m<1

a, đồng biến khi m - 1 > 0 <=> m > 1 

b, nghịch biến khi 3 - m < 0 <=> m > 3 

c, nghịch biến khi m^2 - m < 0 <=> m(m-1) < 0 

Ta có m - 1 < m 

\(\left\{{}\begin{matrix}m-1< 0\\m>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 1\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)

Bài 2 

Với x < 0 thì hàm số trên nghịch biến do m^2 + 1 > 0 

\(y'=3x^2-2\left(2m+1\right)x+m^2+2m=\left(x-m\right)\left(3x-m-2\right)\)

\(y'=0\Rightarrow\left[{}\begin{matrix}x=m\\x=\dfrac{m+2}{3}\end{matrix}\right.\)

TH1: \(m=\dfrac{m+2}{3}\Rightarrow m=1\) hàm đồng biến trên R (thỏa mãn)

TH2: \(m< \dfrac{m+2}{3}\Rightarrow m< 1\) hàm đồng biến trên khoảng đã cho khi \(\dfrac{m+2}{3}\le0\Rightarrow m\le-2\)

TH3: \(m>\dfrac{m+2}{3}\Rightarrow m>1\) hàm đồng biến trên khoảng đã cho khi \(m\le0\) (ktm)

Vậy \(\left[{}\begin{matrix}m=1\\m\le-2\end{matrix}\right.\)

Đáp án A

Phương pháp:

Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.

Cách giải:

*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và  f c 2

*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số  y = x 3

*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.

Chú ý khi giải:

HS thường nhầm lẫn:

- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.

- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.

\(a,\Leftrightarrow\sqrt{\dfrac{m-2}{m+3}}>0\)

Mà \(\sqrt{\dfrac{m-2}{m+3}}\ge0\Leftrightarrow\sqrt{\dfrac{m-2}{m+3}}\ne0\Leftrightarrow m\ne2;m\ne-3\)

\(b,y=m^2x-5mx-6m=x\left(m^2-5m\right)-6m\)

Đồng biến \(\Leftrightarrow m^2-5m>0\Leftrightarrow m\left(m-5\right)>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>5\end{matrix}\right.\)

\(c,y=x\left(\dfrac{m+5}{m-2}-1\right)+\sqrt{m-2}=\dfrac{7}{m-2}x+\sqrt{m-2}\)

Đồng biến \(\Leftrightarrow\dfrac{7}{m-2}>0\Leftrightarrow m-2>0\Leftrightarrow m>2\)