Lập trình nhập vào a, b. Giải phương trình bậc nhất: ax + b = 0
lập trình python nhé
Để viết chương trình giải phương trình bậc nhất có dạng: ax + b = 0 (a#0), em cần phải thực hiện lệnh nhập vào từ bàn phím các biến nào sau đây:
A. readln(a, b, x);
B. readln(a, b);
C. readln(a,x);
D. readln(b, x);
viết phương trình python tìm nghiệp của phương trình ax+b=0 với a, b là hai số nguyên được nhập từ bàn phím. In ra " phương trình vô số nghiệm", " phương trình vô nghiệm" cho các trường hợp tương ứng. Nếu có nghiệm thì lấy 4 chữ số sau dấu phẩy
Viết chương trình giải phương trình ax+b=0 với a,b khác 0 được nhập vào từ bàn phím
uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
(C++)
#include <bits/stdc++.h>
using namespace std;
int main() {
int a, b;
double x;
cin >> a >> b;
cout << a << "x+" << b << "=0";
cout << "\n<=> x=" << (double)-b/a << endl;
return 0;
}
Chúc bn học tốt!
Bài đầy đủ hơn của mk (bn có thể tham khảo):
#include <bits/stdc++.h>
using namespace std;
int main() {
int a, b;
double x;
cin >> a >> b;
if(a==0) {
{if(b!=0)
cout << "Phuong trinh vo nghiem" << "\n";}
{if(b==0)
cout << "Phuong trinh co vo so nghiem" << "\n";} }
if (a!=0) {
{ if(b!=0)
{cout << a << "x+" << b << "=0";
cout << "\n<=> x=" << (double)-b/a << "\n";} }
{
if(b==0) {
{
cout << "x=0" << endl;}
}
}
}
return 0;
}
Chúc bn học tốt!
Em hãy ghép các khối lệnh a, b, c, d vào các vị trí tương ứng 1, 2, 3, 4 ở Hình 14.8 để được thuật toán giải phương trình ax + b = 0 trong ngôn ngữ lập trình Scratch với các giá trị a, b nhập từ bàn phím.
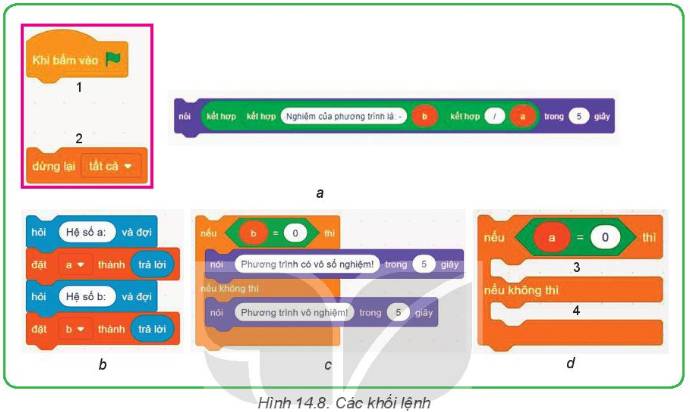
Tham khảo:
Thuật toán giải phương trình ax + b = 0
- Bằng liệt kê tuần tự
Bước 1: Nhập hai số thực a, b
Bước 2. Nếu a = 0
Bước 2.1. Nếu b ≠0 thì thông báo phương trình vô định, rồi kết thúc;
Bước 2.2. Nếu b = 0 thì gán x
Bước 3: x
Bước 4. Đưa ra nghiệm x, rồi kết thúc.
- Sơ đồ khối:
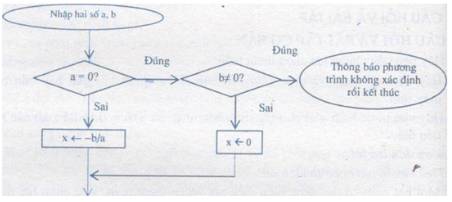
Đề xuất các test tiêu chuẩn
Để xét tất cả các trường hợp có thể xảy ra, ta sử dụng ba bộ test như sau:
i) a = 0, b = 1 (kiểm tra trường hợp phương trình vô định);
ii) a = 0,b = 0 (kiểm tra trường hợp nghiệm x=0);
iii) a = 3, b = 6 (kiểm tra trường hợp nghiêm , y = -b/a).
Viết thuật toán (bằng cách liệt kê các bước) giải bài toán giải bất phương trình ax+b>0 với a,b là số thực. Sau đó viết chương trình (dùng NNLT Python) giải bài toán đó
Chương trình giải phương trình bậc nhất ax+b=0. Em hãy xác định biến của chương trình trên là những biến nào? (chọn đáp án đúng nhất)
A. a, b, x C. a, b
B. x D. a, b, 0
viết phương trình bật nhất có dạng ax+b=0. viết chương trình nhập vào hai tham số a và b. hãy biện luận theo a, b để biết nghiệm của chương trình
1. Thế nào là hai phương trình tương đương? Nêu các quy tắc biến đổi tương đương.
2. Thế nào là phương trình bậc nhất một ẩn? Nêu công thức nghiệm của phương trình bậc nhất một ẩn.
3. Nêu cách giải phương trình đưa được về phương trình dạng ax + b = 0.
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
Tham Khao :
1.
a. Định nghĩa: Hai phương trình gọi là tương đương nếu chúng có cùng một tập hợp nghiệm.
b. Hai quy tắc biến đổi tương đương các phương trình:
2.
Phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn. Ví dụ: Phương trình 5x – 2 = 0 là phương trình bậc nhất ẩn x. Phương trình y – 8 = 4 là phương trình bậc nhất ẩn y.
3.
Để giải các phương trình đưa được về ax+b=0 a x + b = 0 ta thường biến đổi phương trình như sau: + Quy đồng mẫu hai vế và khử mẫu. + Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax+b=0 a x + b = 0 hoặc ax=−b a x = − b .
Dựa vào vị trí tương đối giữa hai đường thẳng dưới đây, hãy tìm mối liên hệ giữa các hằng số a, b, c và các hằng số a’, b’, c’ để hệ phương trình a x + b y = c a ' x + b ' y = c '
Có nghiệm duy nhất
Áp dụng:
Lập một hệ hai phương trình bậc nhất hai ẩn có nghiệm duy nhất.
Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
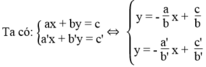
Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có hệ số góc khác nhau:
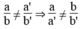
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
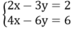
Vì 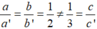 nên hệ phương trình trên vô nghiệm
nên hệ phương trình trên vô nghiệm