viết phương trình các cạnh của hcn cơ sở elip x2/1 + y2/2/3 = 1

Những câu hỏi liên quan
Viết phương trình hình chữ nhật cơ sở của Elip x2/1 + y2/2/3 = 1 Giúp mình với ạ
viết phương trình các cạnh của hcn cơ sở elip 2x3 + 3y2 = 2
Cho elip có phương trình 4 x 2 + 9 y 2 = 36. Khi đó, hình chữ nhật cơ sở có diện tích bằng:
A. 6
B. 12
C. 24
D. 36
Đáp án: C
4 x 2 + 9 y 2 = 36
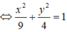
Elip có a 2 = 9 ⇒ a = 3, b 2 = 4 ⇒ b = 2
Hình chữ nhật cơ sở có hai cạnh là 2a = 6, 2b = 4. Do đó, diện tích hình chữ nhật cơ sở là: 6.4 = 24
Đúng 0
Bình luận (0)
Viết phương trình chính tắc của elip (E) biết đỉnh nằm trên trục lớn là (5;0) và đường tròn: x2 +y2= 34 qua 4 đỉnh của HCN cơ sở của elip
Cho Elip (E): 4 x 2 + 5 y 2 = 20. Diện tích hình chữ nhật cơ sở của E là:
A. 2 5
B. 80
C. 8 5
D.40
Đáp án: C
(E): 4
x
2
+ 5
y
2
= 20 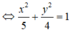
Ta có: a 2 = 5 ⇒ a = 5 , b 2 = 4 ⇒ b = 2
Hình chữ nhật cơ sở có độ dài hai cạnh lần lượt là 2a = 2 5 , 2b = 4
Suy ra, diện tích hình chữ nhật cơ sở là: 2 5 .4 = 8 5
Đúng 0
Bình luận (0)
Phương trình
x
2
m
2
+
y
2
36
1
là phương trình chính tắc của elip có hình chữ nhật cơ sở với diện tích bằng 300 thì: A.
m
±
5
2
B.
m
±
15
2...
Đọc tiếp
Phương trình x 2 m 2 + y 2 36 = 1 là phương trình chính tắc của elip có hình chữ nhật cơ sở với diện tích bằng 300 thì:
A. m = ± 5 2
B. m = ± 15 2
C. m = ± 25 2
D. Không tồn tại m
Cho elip có phương trình 4 x 2 + 9 y 2 = 1 . Khi đó hình chữ nhật cơ sở có diện tích bằng:
A. 6
B. 1/6
C. 24
D. 2/3
viết phương trình chính tắc của elip các trường hợp sau 1. elip đi qua điểm M(0;3) và có tiêu điểm F2(5;0) 2. Elip đi qua hai điểm A(7;0), B(0;3) 3. Elip đi qua hai điểm A(0;1), N(1; căn 3 / 2)
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1
Đúng 2
Bình luận (0)
Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4;3) A. B. C. D.
Đọc tiếp
Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4;3)
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Gọi phương trình chính tắc của Elip có dạng
![]()
Các đỉnh của hình chữ nhật cơ sở có tọa độ: (a; b) ; (a; -b) ; ( -a; b) và (-a; -b)
Ta có M( 4;3) là một đỉnh của hình chữ nhật cơ sở nên chọn
![]() .
.
=> phương trình chính tắc của (E) là

Chọn A.
Đúng 0
Bình luận (0)









