
Những câu hỏi liên quan
GIẢI GIÚP MÌNH PT NÀY BẰNG CÁCH ĐẶT ẨN 2X/(X^2-3X+5) +7X/(X^2-6X+5)=2
Giải phương trình bằng cách đặt ẩn phụ:
\(\left(x^2+5x+8\right)\left(x^2+6x+8\right)=2x^2\)
\(\Leftrightarrow\left(x^2+8+5x\right)\left(x^2+8+6x\right)=2x^2\)
\(\Leftrightarrow\left(x^2+8\right)^2+11x\left(x^2+8\right)+30x^2-2x^2=0\)
\(\Leftrightarrow\left(x^2+8\right)^2+11x\left(x^2+8\right)+28x^2=0\)
\(\Leftrightarrow\left(x^2+4x+8\right)\left(x^2+7x+8\right)=0\)
\(\Leftrightarrow x^2+7x+8=0\)
\(\text{Δ}=49-32=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-7-\sqrt{17}}{2}\\x_2=\dfrac{-7+\sqrt{17}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình sau bằng cách đặt ẩn phụ :
\(\sqrt{x^2+2x+3}-\sqrt{x^2+3x}=3-x\)
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:
7
x
-
y
+
2
-
5
x
+
y
-...
Đọc tiếp
Giải các hệ phương trình sau bằng cách đặt ẩn số phụ: 7 x - y + 2 - 5 x + y - 1 = 4 , 5 3 x - y + 2 + 2 x + y - 1 = 4
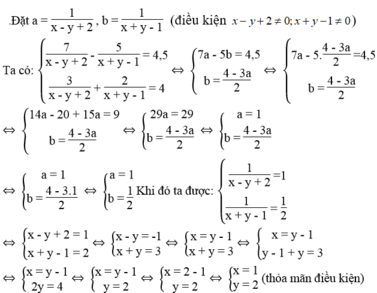
Vậy nghiệm của hệ phương trình là (x; y) = (1; 2).
Đúng 0
Bình luận (0)
Giả pt bằng cách đặt ẩn phụ a,\(2x^2-6x+1=\sqrt{4x+5}\)
b,\(x+\sqrt{5+\sqrt{x-1}=6}\)
c,\(x^2+\sqrt[3]{x^4-x^2}=2x+1\)
d,\(3x^2+21x+18+2\sqrt{x^2+7x+7}=2\)
Giải các phương trình sau bằng phương pháp đặt ẩn phụ:
a,\(x+\sqrt{5+\sqrt{x-1}}=\)6
b,\(x^2+2x\sqrt{x-\frac{1}{x}}=3x+1\)
c,\(\sqrt{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}=2\)
d,\(2x^2-6x-1=\sqrt{4x+5}\)
a) dat x-1=a
x=a+1
\(a+1+\sqrt{5+\sqrt{a}}=6\)
\(5-a=\sqrt{5+\sqrt{a}}\)
\(25-10a+a^2=5+\sqrt{a}\)
\(20-10a+a^2-\sqrt{a}=0\)
(a - \sqrt{5} - 5) (a + \sqrt{a} - 4) = 0
Đúng 0
Bình luận (0)
ý c) dk tu viet
\(\left(\sqrt{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}\right)^2=4\)
\(x-\sqrt{x^2-1}+x+\sqrt{x^2-1}+2\sqrt{\left(x-\sqrt{x^2-1}\right)\left(x+\sqrt{x^2-1}\right)}=4\)
\(2x+2\sqrt{x^2-x^2+1}=4\)
\(2x+2=4\)
2x=2
x=1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giải phương trình sau bằng phương pháp đặt ẩn phụ:
1) \(2\left(3x+5\right)\sqrt{x^2+9}=3x^2+2x+30\)
2) \(2\sqrt[3]{x-2}+\sqrt{x+1}=3\)
giải phương trình căn ( 2x-1) + căn (x-2) = căn (x+1) (bằng cách liên hợp hoặc đặt ẩn phụ)
Đặt: \(\sqrt{2x-1}=a;\sqrt{x-2}=b\Rightarrow\sqrt{x+1}=\sqrt{\left(2x-1\right)-\left(x-2\right)}=\sqrt{a^2-b^2}\)
\(pt\Leftrightarrow a+b=\sqrt{a^2-b^2}\)
\(\Leftrightarrow a^2+2ab+b^2=a^2-b^2\)
\(\Leftrightarrow2b^2+2ab=0\Leftrightarrow2b\left(a+b\right)=0\)
Đúng 2
Bình luận (0)
Giải phương trình sau bằng cách đặt ẩn phụa)
x
2
−
5
x
+
5
−
2
x
2
+
10
x
−
11
.
b)
3
x
2
+
3
x...
Đọc tiếp
Giải phương trình sau bằng cách đặt ẩn phụ
a) x 2 − 5 x + 5 = − 2 x 2 + 10 x − 11 .
b) 3 x 2 + 3 x = x + 5 2 − x + 6 .
















