Giải hệ phương trình sau: x+3y=4 3x-2y=1

Những câu hỏi liên quan
Giải các hệ phương trình sau:
x
+
3
y
4
y
-
x
+
5
2
x
-
y...
Đọc tiếp
Giải các hệ phương trình sau: x + 3 y = 4 y - x + 5 2 x - y = 3 x - 2 y + 1
giải các hệ phương trình
9x-6y=4 và 3(4x-3y)=-3x+y+7
3(x+1)+2y=-x và 5(x+y)=-3x+y-5
2(2x+3y)=3(2x-3y)+10 và 4x-3y=4(6y-2x)+3
Giải hệ phương trình sau bằng phương pháp thế
1) \(\left\{{}\begin{matrix}x-2y=4\\-2x+5y=-3\end{matrix}\right.\)
2) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\)
3) \(\left\{{}\begin{matrix}x+2y=4\\-3x+y=7\end{matrix}\right.\)
\(1,\Leftrightarrow\left\{{}\begin{matrix}x=2y+4\\-4y-8+5y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\cdot5+4=14\\y=5\end{matrix}\right.\\ 2,\Leftrightarrow\left\{{}\begin{matrix}5x-30+6x=3\\y=10-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\\ 3,\Leftrightarrow\left\{{}\begin{matrix}x=4-2y\\6y-12+y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{10}{7}\\y=\dfrac{19}{7}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a
)
x
+
y
2
3
x
+
3
y...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a ) x + y = 2 3 x + 3 y = 2 b ) 3 x − 2 y = 1 − 6 x + 4 y = 0
a) (I): 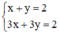
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x + 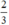 có a’ = -1 ; b’ =
có a’ = -1 ; b’ = 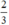
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.
b) (II): 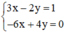
Xét: (d): 3x – 2y = 1 hay (d):
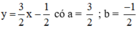
(d’): -6x + 4y = 0 hay (d’):
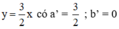
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 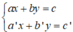
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau:
a) 2x-y=1
3x+2y=5
b) 4x+3y=-1
3x-2y=2
\(a,\left\{{}\begin{matrix}2x-y=1\\3x+2y=5\end{matrix}\right.\\ =>\left\{{}\begin{matrix}4x-2y=2\\3x+2y=5\end{matrix}\right.\\ =>\left\{{}\begin{matrix}7x=7\\2x-y=1\end{matrix}\right.\\ =>\left\{{}\begin{matrix}x=1\\2.1-y=1\end{matrix}\right.\\ =>\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(1;1\right)\)
\(b,\left\{{}\begin{matrix}4x+3y=-1\\3x-2y=2\end{matrix}\right.\\ =>\left\{{}\begin{matrix}4.2x+3.2y=-1.2\\3.3x-2.3y=2.3\end{matrix}\right.\\ =>\left\{{}\begin{matrix}8x+6y=-2\\9x-6y=6\end{matrix}\right.\\ =>\left\{{}\begin{matrix}17x=4\\3x-2y=2\end{matrix}\right.\\ =>\left\{{}\begin{matrix}x=\dfrac{4}{17}\\y=-\dfrac{11}{17}\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(\dfrac{4}{17};-\dfrac{11}{17}\right)\)
Đúng 2
Bình luận (0)
Giải phương trình và hệ phương trình:
1) \(-2x^2+x+1-2\sqrt{x^2+x+1}=0\)
2) \(\left\{{}\begin{matrix}x^4+y^3x+x^2y^2=3y^4\\2x^2+y^4+1=2x\left(y^2+1\right)\end{matrix}\right.\)
1) \(-2x^2+x+1-2\sqrt[]{x^2+x+1}=0\)
\(\Leftrightarrow2\sqrt[]{x^2+x+1}=-2x^2+x+1\left(1\right)\)
Ta có :
\(2\sqrt[]{x^2+x+1}=2\sqrt[]{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\ge\sqrt[]{3}\)
Dấu "=" xảy ra khi và chỉ khi \(x+\dfrac{1}{2}=0\Leftrightarrow x=-\dfrac{1}{2}\)
\(\left(1\right)\Leftrightarrow-2x^2+x+1=\sqrt[]{3}\)
\(\Leftrightarrow2x^2-x+\sqrt[]{3}-1=0\)
\(\Delta=1-8\left(\sqrt[]{3}-1\right)=9-8\sqrt[]{3}\)
\(pt\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt[]{9-8\sqrt[]{3}}}{4}\left(loại\right)\\x=\dfrac{1-\sqrt[]{9-8\sqrt[]{3}}}{4}\left(loại\right)\end{matrix}\right.\) \(\left(vì.x=-\dfrac{1}{2}\right)\)
Vậy phương trình cho vô nghiệm
Đúng 2
Bình luận (0)
giải các hệ phương trình sau
a.{ x + 3y = -2
{ 5x - 4y = 11
b.{ 3xy = 5
{ 5x + 2y = 23
c.{ 3x +5y = 1
{ 2x - y = -8
d.{ x - 2y + 6 = 0
{ 5x - 3y - 5 = 0
e.{ 2(x + y) + 3(x - y) = 4
{ (x + y) + 2(x - y) = 5
\(a,\Leftrightarrow\left\{{}\begin{matrix}5x+15y=-10\\5x-4y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19y=-21\\5x-4y=11\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{21}{19}\\5x-4\left(-\dfrac{21}{19}\right)=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{25}{19}\\y=-\dfrac{21}{19}\end{matrix}\right.\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\10x-5y=-40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\13x=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=2\end{matrix}\right.\\ d,\Leftrightarrow\left\{{}\begin{matrix}5x-10y=-30\\5x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-3y=5\\-7y=-35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=5\end{matrix}\right.\\ e,\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\2\left(x+y\right)+4\left(x-y\right)=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=6\\2\left(x+y\right)+3\cdot6=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=6\\x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{13}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Giải hệ phương trình sau:
\(\hept{\begin{cases}x-3y+\sqrt{x^2+3y^2}=0\\\sqrt{2y-1}+2x^2-y^2-3x+1=0\end{cases}}\)
\(\hept{\begin{cases}x-3y+\sqrt{x^2+3y^2}=0\left(1\right)\\\sqrt{2y-1}+2x^2-y^2-3x+1=0\left(2\right)\end{cases}}\) \(\left(ĐKXĐ:y\ge\frac{1}{2}\right)\)
Xét phương trình (1)
\(\sqrt{x^2+3y^2}=3y-x\)
\(\Rightarrow x^2+3y^2=x^2-6xy+9y^2\)
\(\Leftrightarrow6y^2-6xy=0\)
\(\Leftrightarrow y\left(y-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y=0\left(ktmđkxđ\right)\\x=y\end{cases}}\)
Thay x=y vào (2) ta đc:
\(\sqrt{2y-1}+2y^2-y^2-3y+1=0\)
\(\Leftrightarrow\sqrt{2y-1}+y^2-3y+1=0\)
\(\Leftrightarrow\left(\sqrt{2y-1}-1\right)+\left(y^2-3y+2\right)=0\)
\(\Leftrightarrow\frac{2y-1-1}{\sqrt{2y-1}+1}+\left(y-2\right)\left(y-1\right)=0\)
\(\Leftrightarrow\left(y-1\right)\left(\frac{2}{\sqrt{2y-1}+1}+y-2\right)=0\)
\(\Rightarrow y=1\left(tmđkxđ\right)\)
Vậy nghiệm của hpt trên là (x;y)=(1;1)
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
a
)
−
5
x
+
2
y
4
6
x...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
a ) − 5 x + 2 y = 4 6 x − 3 y = − 7 b ) 2 x − 3 y = 11 − 4 x + 6 y = 5 c ) 3 x − 2 y = 10 x − 2 3 y = 3 1 3
(Các phần giải thích học sinh không phải trình bày).
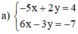 (Nhân 2 vế pt 1 với 3; nhân pt 2 với 2 để hệ số của y đối nhau)
(Nhân 2 vế pt 1 với 3; nhân pt 2 với 2 để hệ số của y đối nhau)
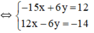 (hệ số của y đối nhau nên ta cộng từ vế 2 pt)
(hệ số của y đối nhau nên ta cộng từ vế 2 pt)
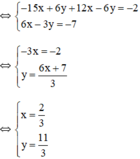
Vậy hệ phương trình có nghiệm duy nhất 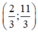
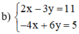 (Nhân hai vế pt 1 với 2 để hệ số của y đối nhau)
(Nhân hai vế pt 1 với 2 để hệ số của y đối nhau)
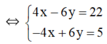 ( lấy vế cộng vế hai phương trình)
( lấy vế cộng vế hai phương trình)
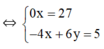
Phương trình 0x = 27 vô nghiệm nên hệ phương trình vô nghiệm.
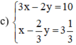 (Nhân hai vế pt 2 với 3 để hệ số của y bằng nhau)
(Nhân hai vế pt 2 với 3 để hệ số của y bằng nhau)
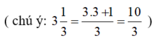
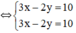 (Trừ từng vế hai phương trình)
(Trừ từng vế hai phương trình)
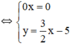
Phương trình 0x = 0 nghiệm đúng với mọi x.
Vậy hệ phương trình có vô số nghiệm dạng 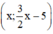 (x ∈ R).
(x ∈ R).
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
Đúng 0
Bình luận (0)

















