tìm x và y để 2x + 5y là số chính phương

Những câu hỏi liên quan
tìm x, y thuộc N để x^2+5y là số chính phương
1. Tìm a,b ∈ Z+(a,b ≠1) để 2a+3b là số chính phương2. Tìm nghiệm nguyên không âm của phương trình:left(2x+5y+1right)left(2020^{left|xright|}+y+x^2+xright)1053. Tìm x,y,z ∈ Z+ t/m: xy+y-x!1;yz+z-y!1;x^2-2y^2+2x-4y24. Tìm tất cả các số nguyên tố p;q;r sao cho: pq+qpr5. Tìm nghiệm nguyên tố của phương trình: x^y+y^x+2022z6. CMR: Với n ∈ N và n2 thì 2n-1 và 2n+1 không thể đồng thời là 2 số chính phương
Đọc tiếp
1. Tìm a,b ∈ Z+(a,b ≠1) để 2a+3b là số chính phương
2. Tìm nghiệm nguyên không âm của phương trình:
\(\left(2x+5y+1\right)\left(2020^{\left|x\right|}+y+x^2+x\right)=105\)
3. Tìm x,y,z ∈ Z+ t/m:
\(xy+y-x!=1;yz+z-y!=1;x^2-2y^2+2x-4y=2\)
4. Tìm tất cả các số nguyên tố p;q;r sao cho:
pq+qp=r
5. Tìm nghiệm nguyên tố của phương trình:
\(x^y+y^x+2022=z\)
6. CMR: Với n ∈ N và n>2 thì 2n-1 và 2n+1 không thể đồng thời là 2 số chính phương
Bài 2: Ta có:
\(\left(2x+5y+1\right)\left(2020^{\left|x\right|}+y+x^2+x\right)=105\) là số lẻ
\(\Rightarrow\left\{{}\begin{matrix}2x+5y+1\\2020^{\left|x\right|}+y+x^2+x\end{matrix}\right.\) đều lẻ
\(\Rightarrow y⋮2\)\(\Rightarrow2020^{\left|x\right|}⋮̸2\Leftrightarrow\left|x\right|=0\Leftrightarrow x=0\).
Thay vào tìm được y...
Đúng 5
Bình luận (0)
Lúc nãy bận thi online nên giờ mới làm tiếp được, bạn thông cảm.
Bài 4:
Do p; q; r là các SNT nên \(p^q+q^p>2^2+2^2=8\Rightarrow r>8\) nên r là SNT lẻ
Mà r lẻ thì trong 2 số \(p^q;q^p\) phải có 1 số lẻ, một số chẵn.
Do vai trò p; q như nhau nên không mất tính tổng quát ta giả sử p lẻ, q chẵn
\(\Rightarrow q=2\). Lúc này ta có:
\(p^2+2^p=r\)
+Xét p=3\(\Rightarrow p^2+2^p=r=17\left(tm\right)\) (Do p lẻ nên loại TH p=2)
+Xét p>3. Ta có:
\(\left\{{}\begin{matrix}p^2\equiv1\left(mod3\right)\\2^p\equiv\left(-1\right)^p\equiv-1\left(mod3\right)\end{matrix}\right.\)
\(\Rightarrow p^2+2^p\equiv1+\left(-1\right)\equiv0\left(mod3\right)\)
\(\Rightarrow\left(p^2+2^p\right)⋮3\) mà \(p^2+2^p>3\) nên là hợp số
\(\Rightarrow r\) là hợp số, không phải SNT, loại.
Vậy ta có \(\left(p;q;r\right)\in\left\{\left(3;2;17\right);\left(2;3;17\right)\right\}\) tm đề bài
Đúng 4
Bình luận (0)
Bài 6: Ta có 1SCP lẻ chia cho 4 dư 1.
Nếu 2n-1 là SCP thì ta có
\(2n-1\equiv1\left(mod4\right)\Leftrightarrow2n+1\equiv3\left(mod4\right)\)
Do đó 2n+1 không là SCP
\(\Rightarrowđpcm\)
Đúng 4
Bình luận (0)
Xem thêm câu trả lời
Bài 1 : Tìm x , y thuộc Z , biết
a ) 21x - 17y = -3
b) 1/x + y/6 = 1/2
GIÚP VỚI !!!!!!!!!!
Bài 2 : Tìm Ước chung lớn nhất của ( 2n - 1 và 9n + 4 )
Bài 3 :
a ) Tìm n để n^2 + 2004 là số chính phương
b) Chứng minh rằng nếu 2x + 3y chia hết cho 17 thì 9x + 5y chia hết cho 17 và ngược lại 9x + 5y chia hết cho 17 thì 2x + 3y chia hết cho 17
Cho các số nguyên dương x , y thoã mãn (2x+3y)^2+5x+5y+1 là số chính phương . Chứng minh rằng x=y
Xem chi tiết
Ta có: \(\left(2x+3y\right)^2< \left(2x+3y\right)^2+5x+5y+1< \left(2x+3y+2\right)^2\).
Do đó để \(\left(2x+3y\right)^2+5x+5y+1\) là số chính phương thì \(\left(2x+3y\right)^2+5x+5y+1=\left(2x+3y+1\right)^2\Leftrightarrow x=y\).
Vậy x = y
Đúng 1
Bình luận (1)
tìm x: a) để x^2-2x-4 là số chính phương b)để x^2-2x+7 là số chính phương
Mode 5 3 trên máy tính Casio fx-570 :
a) a=1,b=-2,c=-4
b) a=1,b=-2,c=7
Đúng 0
Bình luận (0)
Tìm giá trị của m để nghiệm của hệ phương trình
x
+
1
3
-
y
+
2
4...
Đọc tiếp
Tìm giá trị của m để nghiệm của hệ phương trình
x + 1 3 - y + 2 4 = 2 x - y 5 x - 3 4 - y - 3 3 = 2 y - x
cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.
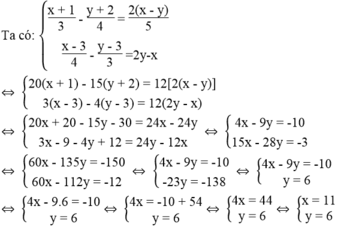
Vì (x; y) = (11; 6) là nghiệm của phương trình 3mx – 5y = 2m +1 nên ta có:
3m.11 – 5.6 = 2m + 1
⇔ 33m – 30 = 2m + 1 ⇔ 31m = 31 ⇔ m = 1
Vậy với m = 1 thì nghiệm của x + 1 3 - y + 2 4 = 2 x - y 5 x - 3 4 - y - 3 3 = 2 y - x cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.
Đúng 0
Bình luận (0)
Cho hệ phương trình \(\hept{\begin{cases}x+2y=m\\2x+5y=1\end{cases}}\), m là tham số
Tìm m để hệ phương trình có nghiệm duy nhất (x,y) sao cho x và y là 2 nghiệm của phương trình \(t^3-\left(3m-t\right)t+m^4+9m-13=0\), t là ẩn số
Bài 1: Tìm x,y thuộc Z thỏa mãn x^2 - 2xy + 5y^2=y+1
Bài 2:Tìm x thuộc Z để số sau là số chính phương
a)x^2 +3x b)x^2 +x+6
Bài 1: Tìm x,y thuộc Z thỏa mãn x^2 - 2xy + 5y^2=y+1
Bài 2:Tìm x thuộc Z để số sau là số chính phương
a)x^2 +3x b)x^2 +x+6
2.
a.
\(x^2+3x=k^2\)
\(\Leftrightarrow4x^2+12x=4k^2\)
\(\Leftrightarrow4x^2+12x+9=4k^2+9\)
\(\Leftrightarrow\left(2x+3\right)^2=\left(2k\right)^2+9\)
\(\Leftrightarrow\left(2x+3\right)^2-\left(2k\right)^2=9\)
\(\Leftrightarrow\left(2x+3-2k\right)\left(2x+3+2k\right)=9\)
| 2x+3-2k | -9 | -3 | -1 | 1 | 3 | 9 |
| 2x+3+2k | -1 | -3 | -9 | 9 | 3 | 1 |
| x | -4 | -3 | -4 | 1 | 0 | 1 |
| nhận | nhận | nhận | nhận | nhận | nhận |
Vậy \(x=\left\{-4;-3;0;1\right\}\)
b. Tương tự
\(x^2+x+6=k^2\)
\(\Leftrightarrow4x^2+4x+24=4k^2\)
\(\Leftrightarrow\left(2k\right)^2-\left(2x+1\right)^2=23\)
\(\Leftrightarrow\left(2k-2x-1\right)\left(2k+2x+1\right)=23\)
Em tự lập bảng tương tự câu trên
Đúng 1
Bình luận (0)
1.
\(\Leftrightarrow x^2-2xy+y^2=-4y^2+y+1\)
\(\Leftrightarrow-4y^2+y+1=\left(x-y\right)^2\ge0\)
\(\Leftrightarrow-64y^2+16y+16\ge0\)
\(\Leftrightarrow\left(8y-1\right)^2\le17\)
\(\Rightarrow\left(8y-1\right)^2\le16\)
\(\Rightarrow-4\le8y-1\le4\)
\(\Rightarrow-\dfrac{3}{8}\le y\le\dfrac{5}{8}\)
\(\Rightarrow y=0\)
Thế vào pt ban đầu:
\(\Rightarrow x^2=1\Rightarrow x=\pm1\)
Vậy \(\left(x;y\right)=\left(-1;0\right);\left(1;0\right)\)
Đúng 1
Bình luận (0)
Tìm số tự nhiên x có hai chữ số để 2x +1 và 3x+1 đều là các số chính phương

















