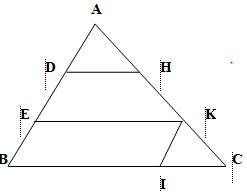
Cho hình vẽ sau, ta có AD = BE,DH // EK // BC. Chứng minh rằng DH + EK = BC ( gợi ý: kẻ IK // AB )
cho tam giác ABC nhọn vẽ phía ngoài tam giác ABC các đoạn thẳng BD=BA và CE=CA kẻ DH,EK vuông góc với đường thẳng BC chứng minh rằng DH+EK=BC
cho tam giác ABC trên AB lấy điểm d ,trên AC lấy điểm e sao cho AD=AE
a, Chứng minh:DE song song với BC
b, kẻ DI uông góc với BC , EK vuông góc với BC . Chứng minh rằng DI=EK
c, trên tia đối của CA lấy điểm H sao cho CH=CE. chứng minh rằng BC cắt DH ttaij trung điểm của DH
bn tự vẽ hình nha
a)tg ABC cân tại A suy ra AB=AC VÀ ABC=ACB
TA CÓ ABC+ACB+BAC=180 SUY RA 2ABC=180-BAC(1)
TA CÓ TG ADE CÂN TẠI A SUY RA AD=AE VÀ ADE=AED
TA CÓ ADE+AED+BAC=180 SUY RA 2ADE=180-BAD(2)
TỪ 1 VÀ 2 SUY RA DE SONG SONG BC
B)CMĐ DI SONG SONG EK
MÀ DE SONG SONG IK
TỪ 2 ĐIỀU TRÊN SUY RA DI=EK(TÍNH CHẤT HÌNH THANG)
C)TỪ H VẼ HN VUÔNG GÓC VỚI BC
MÀ DI VUÔNG GÓC VỚI BC
TỪ 2 ĐIỀU TRÊN SUY RA DI SONG SONG HN SUY RA IDH=NHD
GỌI G LÀ GIAO ĐIỂM CỦA DH VÀ IN
CMĐ TG DIB=NHC(CH GN)
CMĐ TG IDK=NHK(C G C)
SUY RA ĐPCM
TỚ GỢI Ý CHO CẬU RÙI ,CẬU TỰ PHĂNG RA NHA
cho tam giác ABC (AB=AC) kẻ tia phân giác BD,CE
a) chứng minh BD=CE
b) kẻ DH vuông góc với BC , EK vuông góc với BC, chứng minh DH song song với EK, DH=EK
c BD cắt CE tại i chứng minh AI vuông góc với BC
a) Xét tam giác ABC ta có AB = AC
=> Tam giác ABC cân tại A
=> \(\widehat{ABC}\)= \(\widehat{ACB}\)
=> \(\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{ACB}\)
=> \(\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)
Xét tam giác ACE và tam giác ABD, ta có:
\(\widehat{A}\) chung
AC = AB (gt)
\(\widehat{ACE}=\widehat{ABD}\)
=> Tam giác ACE = tam giác ABD (g.c.g)
=> BD = CE
b) Ta có: \(\hept{\begin{cases}DH⊥BC\\EK⊥BC\end{cases}}\)
=> DH // EK
Xét tam giác DHB vuông tại H và
tam giác EKC vuông tại K, ta có:
BD = CE (cmt)
\(\widehat{DBH}\)(hay \(\widehat{DBC}\)) = \(\widehat{ECK}\)(hay \(\widehat{ECB}\)) (cmt)
=> Tam giác DHB = tam giác EKC (ch.gn)
=> DH = EK
Còn câu c mình không biết
a)Tam giác ABC có AB=AC suy ra tam giác ABC cân tại A suy ra góc B = C
Mà BD là tia phân giác của góc B ; CE là tia phân giác của góc C
suy ra góc ABD = CBD =BCE =ACE
Xét tam giác ABD và ACE có :
góc ABD =góc ACE (cmt )
AB = AC (gt)
Chung gócA
suy ra tam giác ABD = ACE (g.c.g )
suy ra BD = CE ( 2 cạnh tương ứng )
b) Ta có DH vuông góc với BC ; EK vuông góc với BC
suy ra DH song song với EK
Xét tam giác CEK và BDH có :
BD= CE ( cm ở ý a)
góc CKE = góc BHD ( = 90 độ )
góc CBD = BCE ( cm ở ý a )
suy ra tam giác CEK= BDH (ch-gn)
suy ra DH = EK ( 2 cạnh tương ứng )
c) Xét tam giác BIC có góc CBD =BCE ( cm ở ý a ) suy ra tam giác BIC cân tại I
suy ra BI = CI ( t/c tam giác cân )
Xét tam giác AIC và AIB có :
AB =AC ( gt )
góc ACE = ABD ( cm ở ý a )
CI = BI ( cmt)
suy ra tam giác AIC = AIB ( c.g.c)
suy ra góc IAC = IAB (2 góc tương ứng )
suy ra AI là tia phân giác của góc BAC (1)
Mà tam giác ABC cân tại A ( 2)
Từ ( 1 ) và ( 2 ) suy ra AI vuông góc với BC
( nếu đúng nhớ kết bạn với tớ nhé ^-^)
Cho tam giác ABC có 3 góc nhọn . Vẽ về phía ngoài của tam giác ABC các đoạn thẳng BD BA BD BA = ⊥ , và CE CA CE CA = ⊥ , . Kẻ DH EK , vuông góc với đường thẳng BC (H và K thuộc đường thẳng BC). Chứng minh rằng : DH EK BC
Cho tam giác ABC có 3 góc nhọn . Vẽ về phía ngoài của tam giác ABC các đoạn thẳng BD=BA BD ⊥BA và CE=CA CE⊥ CA Kẻ DH EK , vuông góc với đường thẳng BC (H và K thuộc đường thẳng BC). Chứng minh rằng :DH+EK=BC
Từ A dựng đường thẳng vuông góc với BC căt BC tại M
Xét tg vuông ABM và tg vuông BDH có
\(BD\perp BA;HB\perp AM\Rightarrow\widehat{HBD}=\widehat{MAB}\) (góc có cạnh tương ứng vuông góc)
\(BD=BA\left(gt\right)\)
\(\Rightarrow\Delta BDH=\Delta ABM\) (hai tg vuông có cạnh huyền và 1 góc nhọn tương ứng bằng nhau)
\(\Rightarrow DH=BM\)
Chứng minh tương tự ta cũng có \(EK=CM\)
\(\Rightarrow DH+EK=BM+CM=BC\left(đpcm\right)\)
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên tia đối của tia CA lấy điểm E sao cho BD = CE. Kẻ DH và EK vuông góc với BC (H,K thuộc BC). Gọi I là giao điểm của BE và BC. Chứng minh rằn a) DH = EK b) I là trung điểm của DE
a, Ta có : \(\Delta\)ABC cân tại A (gt)
\(\Rightarrow\)Góc B = góc \(C_1\)
Mà góc \(C_1=C_2\)(đối đỉnh)
\(\Rightarrow\)Góc B = góc \(C_2\)
Xét \(\Delta BDH\)\(\perp H\)(DH\(\perp\)BC) và \(\Delta CEK\perp K\)(EK \(\perp\)BC) có :
BD=CE (gt)
Góc B = góc C\(_2\)(cmt)
\(\Rightarrow\Delta BDH=\Delta CEK\)(ch-gn)
\(\Rightarrow DH=EK\)( 2 cạnh tg ứng)
Vậy...
b, Ta có : DH và EK cùng vuông góc vs BC (gt)
\(\Rightarrow\)DH \(//\)EK (Quan hệ từ vuông góc đến song song)
\(\Rightarrow\)Góc HDI = góc IEC ( 2 góc so le trong )
Xét \(\Delta HDI\perp H\left(DH\perp BC\right)\)và \(\Delta KEI\perp K\left(EK\perp BC\right)\)có :
DH=CE (\(\Delta BEH=\Delta CEK\))
Góc HDI = góc IEC (cmt)
\(\Rightarrow\)\(\Delta HDI=\Delta KEI\)(cgv-gnk)
\(\Rightarrow DI=EI\)( 2 cạnh tg ứng )
Mà D,I,E thẳng hàng ( DE và BC cắt nhau tại I )
\(\Rightarrow\)I là trung điểm của BC
Vậy...
Chúc bn hok tốt
Cho tam giác ABC cân tại A lấy D trên AB, lấy E trên AC sao cho BD=CE . Kẻ các đường vuông góc DH vuông góc BC . EK vuông góc BC a) Chứng mình DH song song EK b) Chứng minh tam giác BDH=CEK
a: DH vuông góc BC
EK vuông góc BC
=>DH//EK
b: góc BDH+góc B=90 độ
góc CEK+góc C=90 độ
góc B=góc C
=>góc BDH=góc CEK
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên tia đối của tia CA lấy điểm E sao cho BD = CE. Kẻ DH và EK vuông góc với BC (H,K thuộc BC). Gọi I là giao điểm của BE và BC. Chứng minh rằn a) DH = EK b) I là trung điểm của DE
Cho ΔABC cân tại A. Trên cạnh đáy BC lấy hai điểm D và E sao cho BD = CE < \(\frac{BC}{2}\)
a. Chứng minh ΔABD = ΔACE
b. Kẻ DH ⊥ AB tại H, EK ⊥ AC tại K. Chứng minh DH = EK
c.Gọi M là một điểm nằm giữa D và E . Chứng inh AM + MB > AD+DH
Cho tam giác ABC cân tại A,kẻ phân giác BD của góc B,kẻ phân giác CE của góc C
1) Chứng minh BD=CE
2) Kẻ Dh vuông góc với BC,EK vuông góc với BC.Chứng minh
a)DH//EK
b)DH=EK
1) Ta có: \(\widehat{ABD}=\widehat{CBD}=\dfrac{\widehat{ABC}}{2}\)(BD là tia phân giác của \(\widehat{ABC}\))
\(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}\)(CE là tia phân giác của \(\widehat{ACB}\))
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{CBD}=\widehat{ACE}=\widehat{BCE}\)
Xét ΔABD và ΔACE có
\(\widehat{BAD}\) chung
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
Do đó: ΔABD=ΔACE(g-c-g)
Suy ra: BD=CE(hai cạnh tương ứng)
2) Ta có: EK⊥BC(gt)
DH⊥BC(gt)
Do đó: EK//DH(Định lí 1 từ vuông góc tới song song)
Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(hai cạnh tương ứng)
Ta có: AE+EB=AB(E nằm giữa A và B)
AD+DC=AC(D nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và AE=AD(cmt)
nên EB=DC
Xét ΔEKB vuông tại K và ΔDHC vuông tại H có
EB=DC(cmt)
\(\widehat{EBK}=\widehat{DCH}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEKB=ΔDHC(cạnh huyền-góc nhọn)
Suy ra: EK=DH(hai cạnh tương ứng)