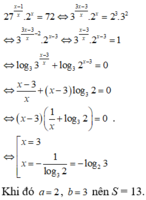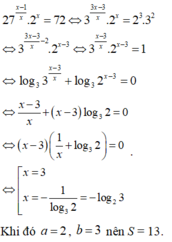viết dưới dạng tích tổng sau : a2 + b2 + 2ab

Những câu hỏi liên quan
Dùng diện tích để chứng tỏ : a + b 2 = a 2 + 2 a b + b 2
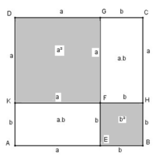
Dựng hình vuông ABCD có cạnh bằng (a + b )
Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F.
Ta có : diện tích hình vuông ABCD bằng a + b 2
Diện tích hình vuông DKFG bằng a 2
Diện tích hình chữ nhật AKFE bằng a.b
Diện tích hình vuông EBHF bằng b 2
Diện tích hình chữ nhật HCGF bằng a.b
S A B C D = S D K F G + S A K E F + S E B H F + S H C G F
Vậy ta có : a + b 2 = a 2 + 2 a b + b 2
Đúng 0
Bình luận (0)
Biết phương trình
27
x
-
1
x
.
2
x
27
có một nghiệm viết dưới dạng
x
-
log
a
b
, với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng
S
a
2
+
b...
Đọc tiếp
Biết phương trình 27 x - 1 x . 2 x = 27 có một nghiệm viết dưới dạng x = - log a b , với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng S = a 2 + b 2 .
A. S = 29
B. S = 25
C. S = 13
D. S = 34
Dùng diện tích để chứng tỏ :
a
-
b
2
a
2
-
2
a
b
+
b
2
với điều kiện b a
Đọc tiếp
Dùng diện tích để chứng tỏ : a - b 2 = a 2 - 2 a b + b 2 với điều kiện b < a
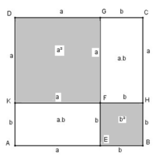
Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng a 2
Hình vuông DKFG có diện tích bằng a - b 2
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng b 2
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
S A B C D = S D K F G + S A E F K = S E B H F + S H C G F
nên a - b 2 + a - b b + a - b b + b 2 = a 2
⇒ a - b 2 = a 2 - 2 a b + b 2
Đúng 0
Bình luận (0)
Địa chỉ ô được viết như sau?
A. A2+B2 B. 2A + 2B C. 2,A + 2,B D. 2AB + 2 BA
Xem thêm câu trả lời
Biết phương trình
27
x
-
1
x
.
2
x
72
có một nghiệm viết dưới dạng
x
-
log
a
b
, với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng
S
...
Đọc tiếp
Biết phương trình 27 x - 1 x . 2 x = 72 có một nghiệm viết dưới dạng x = - log a b , với a, b là các số nguyên dương nhỏ hơn 8. Khi đó tính tổng S = a 2 + b 2
A. S = 29
B. S = 25
C. S = 13
D. S = 34
Đa thức
25
–
a
2
+
2
a
b
–
b
2
được phân tích thành A. (5 + a – b)(5 – a – b) B. (5 + a + b)(5 – a – b) C. (5 + a + b)(5 – a + b) D. (5 + a – b)(5 – a + b)
Đọc tiếp
Đa thức 25 – a 2 + 2 a b – b 2 được phân tích thành
A. (5 + a – b)(5 – a – b)
B. (5 + a + b)(5 – a – b)
C. (5 + a + b)(5 – a + b)
D. (5 + a – b)(5 – a + b)
Ta có
25 – a 2 + 2 a b – b 2 = 25 – ( a 2 – 2 a b + b 2 ) = 5 2 – ( a – b ) 2
= (5 + a – b)(5 – a + b)
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?A. (A – B)2 A2 – 2AB + B2 B. (A + B)2 A2 + 2AB + B2C. A2 – B2 (A + B)(A – B) D. A3 – B3 (A – B)(A2 + AB + B2)
Đọc tiếp
Để tính giá trị biểu thức 20212 – 212 theo phương pháp dùng hằng đẳng thức thì áp dụng hằng đẳng thức nào sau đây?
A. (A – B)2 = A2 – 2AB + B2
B. (A + B)2 = A2 + 2AB + B2
C. A2 – B2 = (A + B)(A – B)
D. A3 – B3 = (A – B)(A2 + AB + B2)
Phân tích đa thức thành nhân tử:
ax – bx – a2 + 2ab – b2
ax - bx - a² + 2ab - b²
= (ax - bx) - (a² - 2ab + b²)
= x(a - b) - (a - b)²
= (a - b)(x - a + b)
Đúng 1
Bình luận (0)
chứng minh các đẳng thức sau
(a-b)2=a2-2ab+b2
(a-b)(a+b)=a2-b2
(a+b)3=a3+3a2b+3ab2+b3
(a-b)^2=(a-b)(a-b)=a^2-ab-ab+b^2=a^2-2ba+b^2
(a-b)(a+b)=a^2+ab-ab-b^2=a^2-b^2
(a+3)^3=(a+b)^2*(a+b)
=(a^2+2ab+b^2)(a+b)
=a^3+a^2b+2a^2b+2ab^2+b^2a+b^3
=a^3+3a^2b+3ab^2+b^3
Đúng 1
Bình luận (0)