Bạn tham khảo:

Cho bất phương trình  x2-6x +2(m+2)|x-3| +m2 +4m +12 >0có bao nhiêu giá trị nguyên của m ϵ [-10;10]  để bất phương tình... - Hoc24

Đồ thị hàm số \(y=f\left(\left|x\right|\right)\)

\(f^2\left(\left|x\right|\right)+\left(m-1\right)f\left(\left|x\right|\right)-m=0\left(1\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}f\left(\left|x\right|\right)=1\left(2\right)\\f\left(\left|x\right|\right)=-m\left(3\right)\end{matrix}\right.\)

Từ đồ thị ta thấy phương trình \(\left(2\right)\) có hai nghiệm phân biệt nên phương trình \(\left(1\right)\) có hai nghiệm phân biệt khi phương trình \(\left(3\right)\) có hai nghiệm phân biệt khác hai nghiệm của phương trình \(\left(2\right)\).

\(\Leftrightarrow\left[{}\begin{matrix}-m=-3\\-1< -m< 1\\-m>1\end{matrix}\right.\)

...

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)

\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)

Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất

\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)

\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)

\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)

\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)

\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)

Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)

\(\Rightarrow\) Có 6 giá trị nguyên của m

\(y'=\dfrac{x-m-x+1}{\left(x-m\right)^2}=\dfrac{1-m}{\left(x-m\right)^2}\)

Hàm số nghịch biến trên khoảng \(\left(-\infty;2\right)\Leftrightarrow y'< 0\forall x\in\left(-\infty;2\right)\Leftrightarrow\left\{{}\begin{matrix}1-m< 0\\x\ne m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ge2\end{matrix}\right.\Rightarrow m\ge2\)

Có 19-2+1=18 giá trị nguyên của m thỏa mãn

Ta có: \(\left(x-2\right)\left(x^2-7x+41\right)=0\)

\(\Leftrightarrow x-2=0\)

hay x=2

Thay x=2 vào (2), ta được:

\(2^2-2m+m^2-5m+8=0\)

\(\Leftrightarrow m^2-7m+12=0\)

\(\Leftrightarrow\left(m-3\right)\left(m-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=3\\m=4\end{matrix}\right.\)

Vậy: Có 2 giá trị nguyên của m thỏa mãn hai phương trình có nghiệm chung

Điều kiện xác định x∈Rx∈R.

Đặt t=√x2+1 (t≥1t≥1)

Phương trình trở thành t2−1−4t−m+1=0

⇔t2−4t=m

⇔t2−4t=m. (1)

Để phương trình có 44 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt lớn hơn 11.

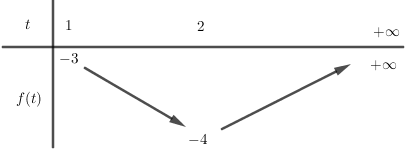
Xét hàm số f(t)=t2−4t có đồ thị là parabol có hoành độ đỉnh x=2∈(1;+∞) nên ta có bảng biến thiên:

Dựa BBT ta thấy để (1) có hai nghiệm phân biệt lớn hơn 11 thì −4<m<−3

Vậy không có giá trị nguyên của mm thỏa mãn yêu cầu bài toán.

Đặt \(\left|x\right|=t\ge0\Rightarrow t^2-4t-m=0\) (1)

Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương pb

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4+m>0\\t_1+t_2=4>0\\t_1t_2=-m>0\end{matrix}\right.\) \(\Leftrightarrow-4< m< 0\Rightarrow m=\left\{-3;-2;-1\right\}\)

1.

\(\Leftrightarrow1-2sin^2x+sinx+m=0\)

\(\Leftrightarrow2sin^2x-sinx-1=m\)

Đặt \(sinx=t\Rightarrow t\in\left[-\dfrac{1}{2};\dfrac{\sqrt{2}}{2}\right]\)

Xét hàm \(f\left(t\right)=2t^2-t-1\) trên \(\left[-\dfrac{1}{2};\dfrac{\sqrt{2}}{2}\right]\)

\(-\dfrac{b}{2a}=\dfrac{1}{4}\in\left[-\dfrac{1}{2};\dfrac{\sqrt{2}}{2}\right]\)

\(f\left(-\dfrac{1}{2}\right)=0\) ; \(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\) ; \(f\left(\dfrac{\sqrt{2}}{2}\right)=-\dfrac{\sqrt{2}}{2}\)

\(\Rightarrow-\dfrac{9}{8}\le f\left(t\right)\le0\Rightarrow-\dfrac{9}{8}\le m\le0\)

Có 2 giá trị nguyên của m (nếu đáp án là 3 thì đáp án sai)

2.

ĐKXĐ: \(sin2x\ne1\Rightarrow x\ne\dfrac{\pi}{4}\) (chỉ quan tâm trong khoảng xét)

Pt tương đương:

\(\left(tan^2x+cot^2x+2\right)-\left(tanx+cotx\right)-4=0\)

\(\Leftrightarrow\left(tanx+cotx\right)^2+\left(tanx+cotx\right)-4=0\)

\(\Rightarrow\left[{}\begin{matrix}tanx+cotx=\dfrac{1+\sqrt{17}}{2}\\tanx+cotx=\dfrac{1-\sqrt{17}}{2}\left(loại\right)\end{matrix}\right.\)

Nghiệm xấu quá, kiểm tra lại đề chỗ \(-tanx+...-cotx\) có thể 1 trong 2 cái đằng trước phải là dấu "+"

Miền \(\left[-\dfrac{\pi}{3};\dfrac{\pi}{2}\right]\) là cung tròn CAB

Chiếu cung tròn lên trục cos (trục ngang) được đoạn màu đỏ, với O có hoành độ bằng 0, A có hoành độ bằng 1

Do đó miền giá trị của cos trên \(\left[-\dfrac{\pi}{3};\dfrac{\pi}{2}\right]\) là \(\left[0;1\right]\) hay đoạn OA

Đặt \(t=x^2-2x+3\left(t\ge2\right)\)

Phương trình trở thành \(f\left(t\right)=t^2+2\left(3-m\right)t+m^2-6m=0\left(1\right)\)

Phương trình \(\left(1\right)\) có nghiệm \(t_1\ge t_2\ge2\) khi:

\(\left\{{}\begin{matrix}\Delta'\ge0\\\dfrac{t_1+t_2}{2}\ge2\\1.f\left(2\right)\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(3-m\right)^2-m^2+6m\ge0\\m-3\ge2\\m^2-10m+16\ge0\end{matrix}\right.\)

Giải ra tập giá trị của m rồi lấy các giá trị thuộc \(\left[-10;10\right]\)