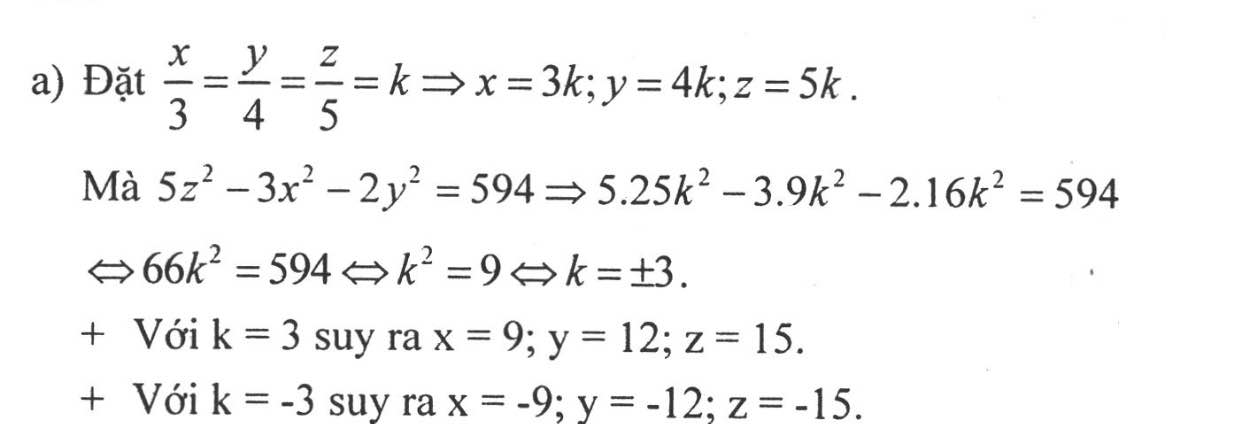tính A = 3x + 2y + 5z và y = x - 3 , z = x - 4 . tính A theo x

Những câu hỏi liên quan
A,Tìm y biết 1+3y/5x =4+7y/15=1+2y/8
B, tìm x,y,z biết 2x=3y,7z=5x và 3x-7y+5z=80
C,cho 3x-2y/4=2z-4x/3=4y-3z/2 c/m x/2=y/3=z/4
D, cho a,b,c not=0 thỏa mãn a+b-c/c=b+c-a/a=c+a-b/b tính B= (1+b/d)(1+a/c)(1+c/b)
E, cho x/3=y/4,y/5= z/6 và 2x + 3y + 4z= 372 tính A = 3x + 4y+5z
G, tính Q=6b-5a/5a+6b
Tìm các số x, y, z biết rằng:
a) x : y : z = 5 : 3 : 4 và x + 2y – z = –126
b) 5x = 2y, 3y = 5z và x + y + z = –970
c) 3x = 4y = 5z và x + y + z = 47
a, Ta có : \(x:y:z=5:3:4\Rightarrow\frac{x}{5}=\frac{y}{3}=\frac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{5}=\frac{y}{3}=\frac{z}{4}=\frac{x+2y-z}{5+6-4}=-\frac{126}{7}=-18\)
\(x=-90;y=-54;z=-72\)
b, \(5x=2y;3y=5z\Rightarrow\frac{x}{2}=\frac{y}{5};\frac{y}{5}=\frac{z}{3}\Rightarrow\frac{x}{2}=\frac{y}{5}=\frac{z}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{3}=\frac{x+y+z}{2+5+3}=-\frac{970}{10}=-97\)
\(x=-194;y=-485;z=-291\)
c, \(3x=4y=5z\Rightarrow\frac{3x}{60}=\frac{4y}{60}=\frac{5z}{60}\Rightarrow\frac{x}{20}=\frac{y}{15}=\frac{z}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{x}{20}=\frac{y}{15}=\frac{z}{12}=\frac{x+y+z}{20+15+12}=\frac{47}{47}=1\)
\(x=20;y=15;z=12\)
Cho A= 91/2-1)(1/3-1)(1/4-1)...(1/2015-1)(1/2016-1). Tính A
Cho x/4=y/7; y/5=z/6. Tính B=(3x-4y+5z)/(x-2y+5z)
Tìm x,y,z biết:
a,6/11.x=9/2y=18/5z và -x+z=-196
b,x-1/2=y+3/4=z-5/6 và 5z-3x-4y=50
c,4/3x-2y=3/2z-4x=2/4y-3z và x+y-z=-10
(Lưu ý:Ko đc sử dụng t/c của dãy tỉ số bằng nhau)
b. Đặt x-1/2 = y+3/4 = z-5/6 = k
=> x = 2k+1
y = 4k -3
z = 6k+5
5z-3x-4y=50 => 5(6k+5)-3(2k+1)-4(4k-3) = 50
=>30k+25-6k-3-16k+12 = 50
=>(30k-6k-16k)+(25-3+12) = 50
=>8k+34 = 50
=>8k = 16
=>k = 2
nên x = 2.2+1 = 5
y = 4.2-3 = 5
z = 6.2+5 = 17
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho các điều kiện sau: x/5 =y/3=z/7 và 3x+2y-5z=12,24. tính x,y và z
Ta có: \(\frac{x}{5}=\frac{y}{3}=\frac{z}{7}=\frac{3x}{15}=\frac{2y}{6}=\frac{5z}{35}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{3x}{15}=\frac{2y}{6}=\frac{5z}{35}=\frac{3x+2y-5z}{15+6-35}=\frac{12,24}{-14}=-\frac{153}{175}\)
B tự tìm x;y;z nhé
Đúng 0
Bình luận (0)
Tính x,y,z biết:
3x=2y;7y=5z và x+z-y=32
3x = 2y <=> x/2 = y/3
7y = 5z <=> y/5 = z/7
x/2 = y/3 <=> x/10 = y/15
y/5 = z/7 <=> y/15 = z/21
=> x/10 = y/15 = z/21
Áp dụng tính chất dãy tỉ số bằng nhau , ta có:
x/10 = y/15 = z/21 = x + z - y/10 + 21 - 15 = 32/16 = 2
x/10 = 2 <=> x = 20
y/15 = 2 <=> y = 30
z/21 = 2 <=> z = 42
Vậy x = 20 ; y = 30 ; z = 42
Đúng 0
Bình luận (0)
Tìm x,y,z biết :
x/4 = y/3; 3y = 5z và x+y+z = 75
3x = 4y; 2y = 5z và x+y-z = 58
\(\frac{x}{4}=\frac{y}{3};3y=5z\) và x + y + z = 75
Ta có: \(\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\3y=5z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\\frac{y}{5}=\frac{z}{3}\end{cases}}\)
=> \(\frac{x}{4}=\frac{y}{3};\frac{y}{5}=\frac{z}{3}\)
=> \(\frac{x}{20}=\frac{y}{15};\frac{y}{15}=\frac{z}{9}\)
=> \(\frac{x}{20}=\frac{y}{15}=\frac{z}{9}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\frac{x}{20}=\frac{y}{15}=\frac{z}{9}=\frac{x+y+z}{20+15+9}=\frac{75}{44}\)
=> \(\hept{\begin{cases}\frac{x}{20}=\frac{75}{44}\\\frac{y}{15}=\frac{75}{44}\\\frac{z}{9}=\frac{75}{44}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{375}{11}\\y=\frac{1125}{44}\\z=\frac{675}{44}\end{cases}}\)
\(3x=4y;2y=5z\)và x + y - z = 58
Ta có : \(\hept{\begin{cases}3x=4y\\2y=5z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\\frac{y}{5}=\frac{z}{2}\end{cases}}\)
=> \(\frac{x}{4}=\frac{y}{3};\frac{y}{5}=\frac{z}{2}\)
Từ \(\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\Rightarrow\frac{x}{20}=\frac{y}{15}\\\frac{y}{5}=\frac{z}{2}\Rightarrow\frac{y}{15}=\frac{z}{6}\end{cases}\Rightarrow\frac{x}{20}=\frac{y}{15}=\frac{z}{6}=\frac{x+y-z}{20+15-6}=\frac{58}{29}=2}\)
=> \(\hept{\begin{cases}\frac{x}{20}=2\\\frac{y}{15}=2\\\frac{z}{6}=2\end{cases}}\Rightarrow\hept{\begin{cases}x=40\\y=30\\z=12\end{cases}}\)
Đúng 0
Bình luận (0)
1. x/2=y/5 và xy = 40 (làm theo 2 cách)
2.x/2=y/3=z/4 và x-2y+3z=16 (làm theo 3 cách)
3.x-1/2=y-2/3=z-3/4 và x-2y+3z =-10 (làm theo 2 cách)
4.2x=3y,5x=7z và 3x-7y+5z=30
1.C1 Ta có : x/2=y/5=>(x/2)^2=(y/5)^2=x/2.y/5=xy/10=40/10=4=>x=4 hoặc -4, y=10 hoặc -10
C2 : Đặt x/2=y/5=k(k khác 0) => x=2k , y=5k
Ta có xy=40=>2k5k=10k^2=40=>k^2=4=>k=-2 hoặc k=2
Với k=-2=>x=-4,y=-10
Với k=2 => x=4,y=10
Vậy
Đúng 0
Bình luận (0)
Toán tỉ lệ thức dễ , đây là 4 phần gồm 4 loại khác nhau
Đúng 0
Bình luận (0)
2 . Các cách khác tự tìm hiểu nha , nhiều cách dễ lắm
C1 Ta có x/2=y/3=2y/6=z/4=3z/12
Áp dụng tính chất dãy tỉ số bằng nhau và x-2y+3z=16 ta được
x/2=2y/6=3z/12=\(\frac{x-2y+3z}{2-6+12}=\frac{16}{8}=2\)
Với x/2=2=>x=4
2y/6=2=>y=6
3z=12=2=>z=8
Vậy
Đúng 0
Bình luận (0)
a, x : y : z = 3 : 4 : 5 và 5z^2 - 3x^2 - 2y^2 = 594