Chứng minh :a-a-b/2=a+b/2
(ảnh2 bị sai ạ)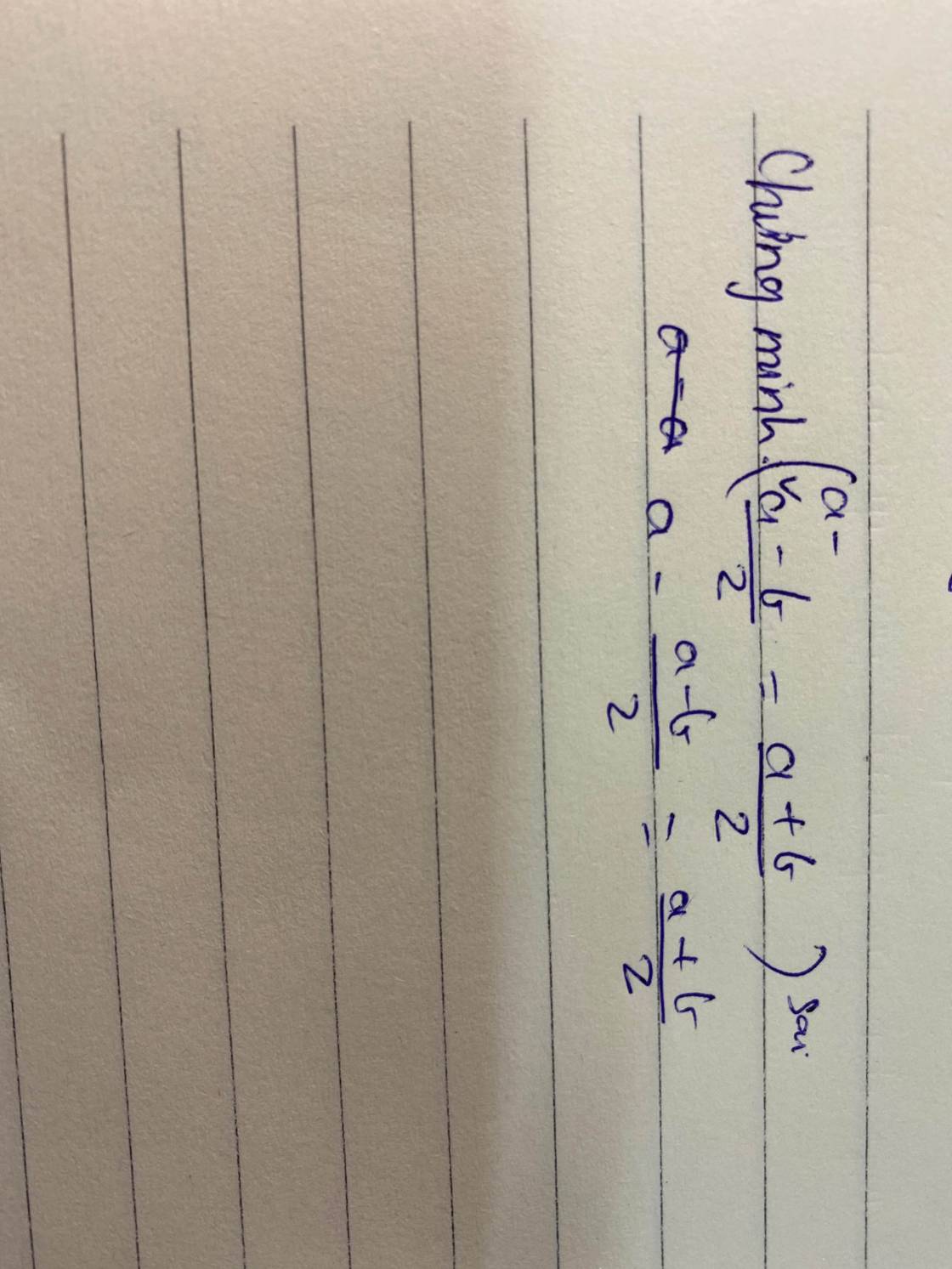
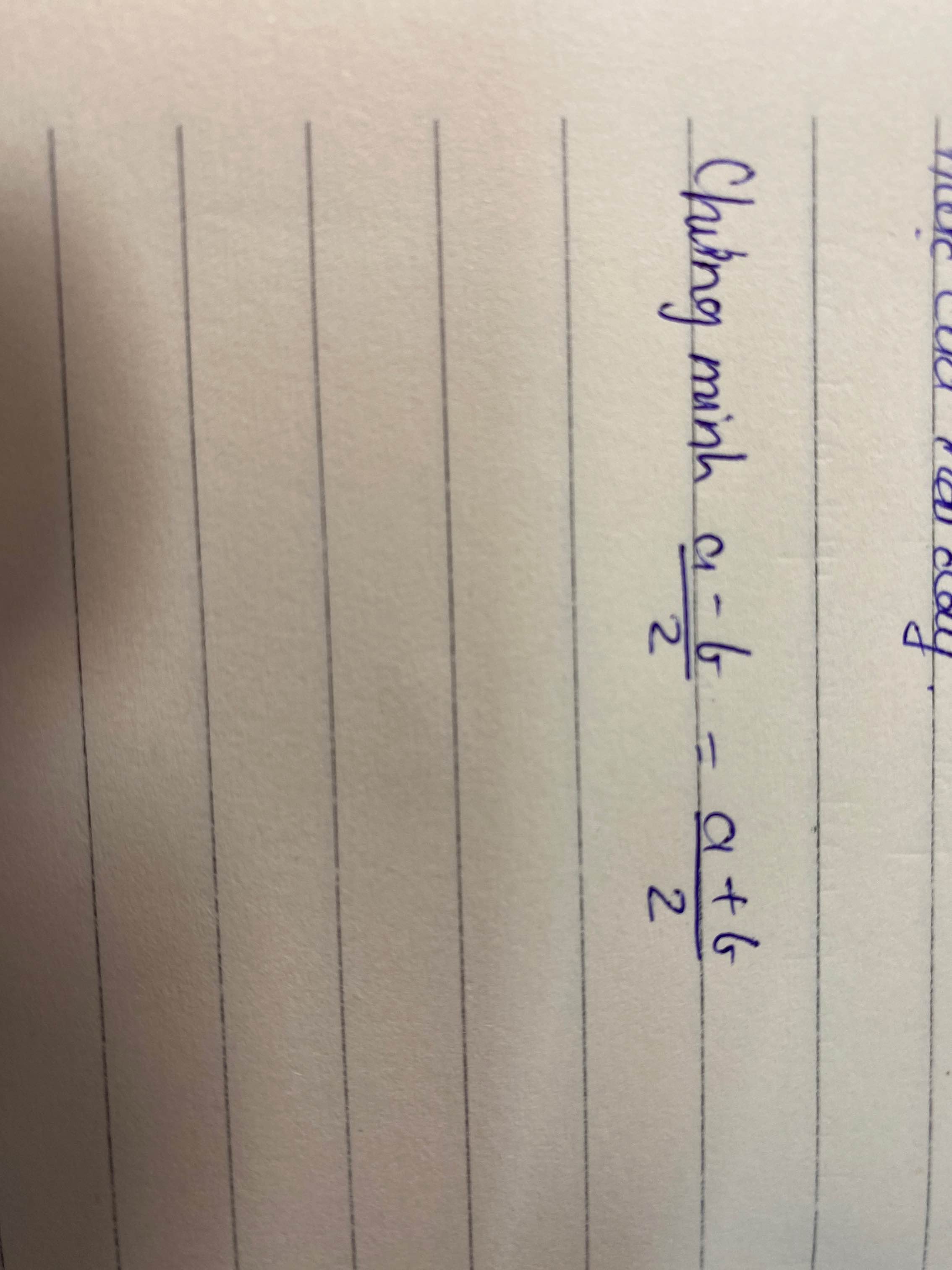
Cho mik hỏi là mik vẽ hình sai á nhma mik chứng minh đúng mà câu A có 2 ý Lan mik chứng minh đúng có bị trừ điểm hông ạ hay là hông có điểm ạ
sẽ bị trừ 1 nửa số điểm vì vẽ hình sai (đó là cô mình sẽ lm, còn cô b thì mình ko bt)
Đề đúng không sai
Cho a,b >0 chứng minh (a+b)^2×[(a+b)/2]≥2a√b + 2b√a
Thế này phải ko?
\(\left(a+b\right)^2.\frac{a+b}{2}\ge2a\sqrt{b}+2b\sqrt{a}\)
ta có: a−√a+14 =(√a−12 )2≥0 (1)
b−√b+14 =(√b−12 )2≥0(2)
từ (1),(2)=.>a+b−√a−√b+12 ≥0
⇒a+b+12 ≥√a+√b (3)
Mà a+b≥2√ab (BĐT cauchy cho a>0;b>0) (4)
từ(3),(4) => (a+b)(a+b+12 )≥2√ab(√a+√b)
⇔(a+b)2+a+b2 ≥2a√b+2b√a
=>đpcm
Cho 3 số dương a,b,c<2. Chứng minh ít nhất một trong các bất đẳng thức sau là sai: a(2-b)>1; b(2-c)>1; c(2-a)>1.
(Gợi ý: Chứng minh bằng phương pháp phản chứng)
Giả sử \(a\left(2-b\right)>1,b\left(2-c\right)>1,c\left(2-a\right)>1\)
\(\Rightarrow abc\left(2-a\right)\left(2-b\right)\left(2-c\right)>1\) (1)
Mặt khác, ta có:
\(a\left(2-a\right)=-a^2+2a=-\left(a-1\right)^2+1\le1\)
Tương tự, \(b\left(2-b\right)\le1,c\left(2-c\right)\le1\)
\(\Rightarrow abc\left(2-a\right)\left(2-b\right)\left(2-c\right)\le1\),điều này trái với (1)
Vậy điều giả sử là sai.
Do đó ít nhất 1 trong 3 bất đẳng thức trên là sai.
Chứng minh rằng nếu a^2+b^2+c^2=ab+ac+bị thì a=b=c
\(a^2+b^2+c^2=ab+bc+ac\)
=> \(2a^2+2b^2+2c^2=2ab+2bc+2ac\)
=>(\(a^2-2ab+b^2\)) +\(\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)\)=0
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
=> a=b=c(DPCM)
Bn ơi đề phải là a2+b2+c2=ab+ac+bc
Ta có
a2+b2+c2=ab+ac+bc
=> 2(a2+b2+c2)=2(ab+ac+bc)
=> 2a2+2b2+2c2=2ab+2ac+2bc
=> 2a2+2b2+2c2-2ab-2ac-2bc=0
=> (a2-2ab+b2)+(b2-2bc+c2)+ (c2-2ca+a2) =0
=> (a-b)2+(b-c)2+(c-a)2=0
=> a-b=b-c=c-a=0
=> a=b=c
=> đpcm
Cho ba số dương a,b,c<2. Chứng minh ít nhất một trong các bất đẳng thức sau là sai: a(2-b)>1; b(2-c)>1; c(2-a)>1.
(Gợi ý: Chứng minh bằng phương pháp phản chứng)
Chứng minh.a,b là 2 số thực tùy ý thì có 1 trong 2 BĐT sau bị sai a²+ab<0,b²+ab<0
Cho a, b tùy ý, chứng minh \(\dfrac{a^2+b^2}{2}\ge ab\)
giúp mik với ạ
Lời giải:
$\frac{a^2+b^2}{2}-ab=\frac{a^2+b^2-2ab}{2}=\frac{(a-b)^2}{2}\geq 0$ với mọi $a,b$
$\Rightarrow \frac{a^2+b^2}{2}\geq ab$ (đpcm)
Chứng minh rằng \(\left(a+b+c\right)^2-\dfrac{3}{4}\left[\left(b-c\right)^2+\left(c-a\right)^2+\left(a-b^2\right)\right]>3\)
với a,b,c là các số thực
Đề có sai ko mọi ngừi
a) Cho a+b+c=0. Chứng minh a3+a2c-abc+b2c+b3=0
b) Cho a-2=x+y. Chứng minh ax+2x+ay+2y+4=a2
c) Cho A=1+x+x2+...x49. Chứng minh Ax-A=x50-1
d) Cho a2+c2=2b2. Chứng minh ( a+b)(a+c)+(c+a)(c+b)=2(b+a)(b+c)
Cần gấp ạ! Ai giải được 4 câu, đúng hết k nhé
a) a3+b3+a2c+b2c-abc
= (a+b)(a2-ab+b2)+c(a2+b2)-abc
=(a+b) [ (a+b)2-3ab]+c.[(a+b)2-2ab]-abc
=(a+b)(a+b)2-3ab(a+b)+c(a+b)2-3abc
=(a+b)2(a+b+c)-3ab(a+b+c)
=(a+b)2.0-3ab.0
=0
b) ax+ay+2x+2y+4
=a(x+y)+2(x+y)+4
=(x+y)(a+2)+4
=(a-2)(a+2)+4
=a2-4+4
=a2
c) A=1+x+x2+...+x49=>Ax=x+x2+x3+...+x50
- A=1+x+x2+...+x49
---> Ax-A=x50-1
d)(a+b)(a+c)+(c+a)(c+b)
=a2+ac+ab+bc+c2+bc+ac+ab
=a2+c2+2ac+2ab+2bc
=2b2+2bc+2ac+2ab
=2b(b+c)+2a(b+c)
=2b(b+c)(b+a)
cho mình hỏi nếu bài hình có 3 câu a,b,c mình làm câu a,b bỏ câu c mà hình vẽ chỉ đáp ứng câu a,b(đề bài c ko vẽ chỉ vẽ a,b yêu cầu) thì có bị trừ điểm ko và nếu chứng minh đúng nhưng ghi sai trường hợp bị trừ nhiều ko ?