vì \(\Delta ABC\)= \(\Delta NPM\)

\(\Rightarrow\)MN = NP  ( 2 cạnh tương ứng )                  ( 1 )

        NP = PM ( 2 cạnh tương ứng )                     ( 2 )

Từ ( 1 ) và ( 2 ) \(\Rightarrow\)MN = NP = PM

Vậy tam giác MNP là tam giác đều

Giải theo ý của mình nhé :

t/g MNP = t/g NPM ( giả thiết )

=> góc M = góc N

góc N = góc P

góc P = góc M 

=> góc M = góc N = góc P

Nên t/g MNP là t/g đều

Ta có \(\Delta MNP=\Delta NPM\)

=> MN = NP (hai cạnh tương ứng)

và NP = PM (hai cạnh tương ứng)

và MP = PM (hai cạnh tương ứng)

=> \(\Delta MNP\)là tam giác đều (theo định nghĩa).

ai đóa giúp mik ik :<

a: Ta có: ΔABC=ΔDEF

nên AB=DE(1)

Ta có: ΔDEF=ΔMNP

nên DE=MN(2)

Từ (1) và (2) suy ra AB=MN

a, Theo định lí Pytago tam giác ABC vuông tại A

\(BC=\sqrt{AB^2+AC^2}=5cm\)

Theo định lí Pytago tam giác MNP vuông tại N

\(NP=\sqrt{MP^2-MN^2}=6cm\)

b, Xét tam giác ABC và tam giác NPM có 

^BAC = ^PNM = 90⁰

\(\dfrac{AB}{NP}=\dfrac{AC}{NM}=\dfrac{3}{6}=\dfrac{4}{8}=\dfrac{1}{2}\)

Vậy tam giác ABC ~ tam giác NPM ( c.g.c ) 

a: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)

\(NP=\sqrt{10^2-8^2}=6\left(cm\right)\)

b: Xét ΔABC vuông tại A và ΔNPM vuông tại N có 

AB/NP=AC/NM

Do đó: ΔABC\(\sim\)ΔNPM

a hí hí giống mk quá

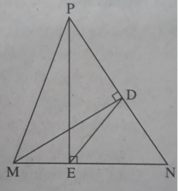
Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên  D N M N = E N P N  Hai tam giác DNE và MNP đồng dạng vì có góc N chung và  D N M N = E N P N