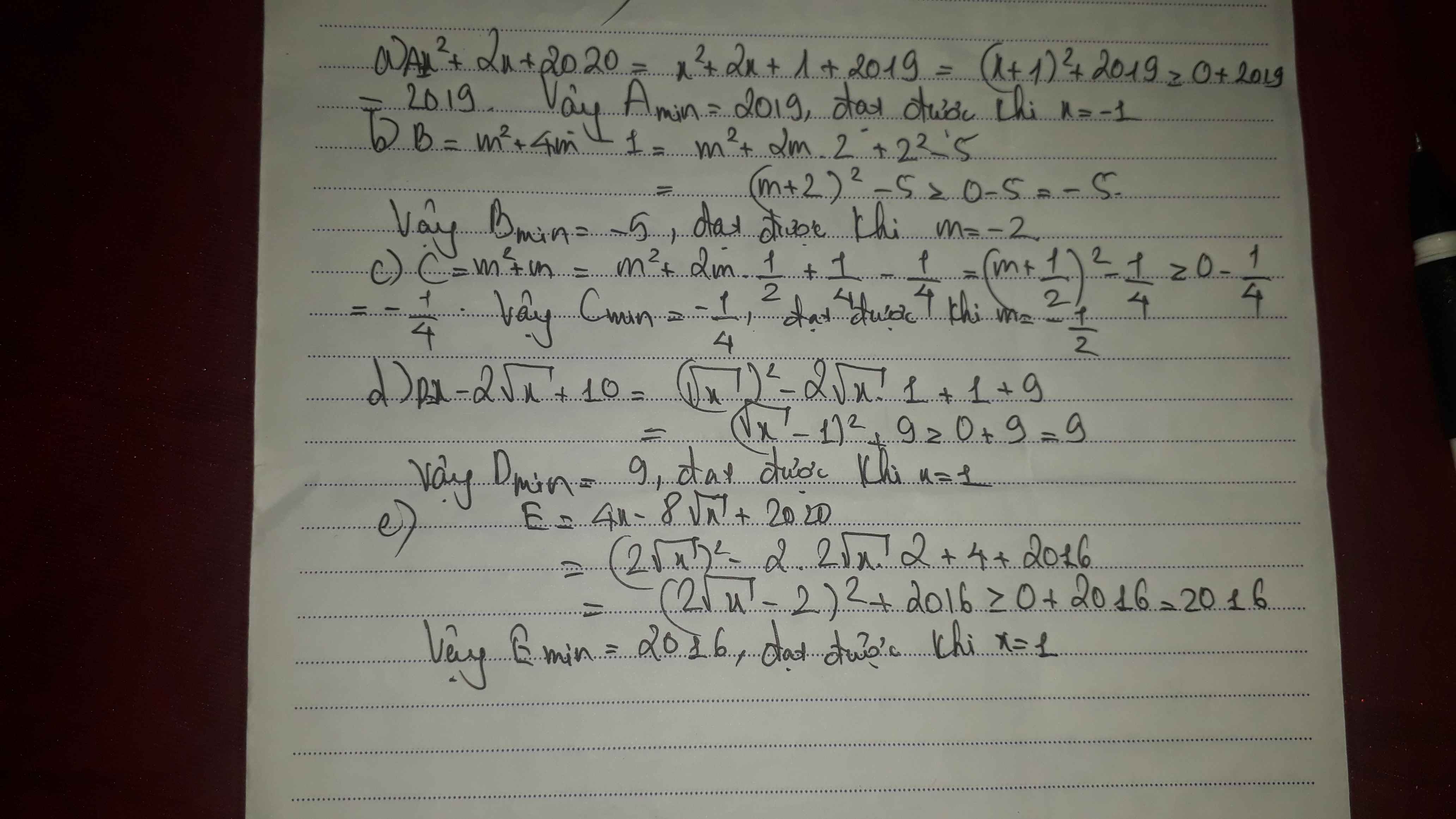Những câu hỏi liên quan
tìm giá trị nhỏ nhất của biểu thức √(m2+2m+1) + √(m2-8m+16)
\(A=\left|m+1\right|+\left|m-4\right|=\left|m+1\right|+\left|4-m\right|>=\left|m+1+4-m\right|=5\)
Dấu = xảy ra khi -1<=m<=4
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A
m
2
+
2
m
+
1
+
m
2
-
8
m
+
16
A. 2 B. 9 C. 5 D. 10
Đọc tiếp
Tìm giá trị nhỏ nhất của biểu thức A = m 2 + 2 m + 1 + m 2 - 8 m + 16
A. 2
B. 9
C. 5
D. 10
Đáp án đúng : C
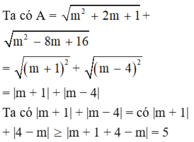
Dấu “=” xảy ra ⇔ m + 1 4 − m ≥ 0
⇔ − 1 ≤ m ≤ 4
Vậy GTNN của A là 5 khi − 1 ≤ m ≤ 4
Đúng 0
Bình luận (0)
Tìm các số nguyên n để giá trị của biểu thức n 3 + 6 n 2 - 7 n + 4 chia hết cho giá trị của biểu thức n - 2.
Tìm các số nguyên n để giá trị của biểu thức n 3 + 6 n 2 - 7 n + 4 chia hết cho giá trị của biểu thức n - 2
Ở đây, ta có thực hiện đặt phép chia như câu 1 để tìm số dư và tìm điều kiện giá trị của n để thỏa mãn đề bài. Nhưng bài này ta làm cách biến đội như sau:

Đúng 0
Bình luận (0)
Tìm GTNN của biểu thức sau:
\(A=\frac{3m^2-2m-1}{\left(m+1\right)^2}\)
Giải từng bước ra được ko @Nguyễn đình quý?
Đúng 0
Bình luận (0)
*Tìm hướng giải: Thông thường khi gặp bài này ta sẽ liên tưởng ngay tới \(\left(m+1\right)^2\ge0\) để từ đó tìm được x và thay vào tử tìm GTNN. Nhưng không được,vì để phân thức có nghĩa thì mẫu khác 0.Ta phải tìm hướng giải khác
*Hướng giải khác; Ta thử phân tích tử xem sao. ĐK \(m\ne-1\)
Ta có: \(3m^2-2m-1\)
\(=3\left(m^2-\frac{2}{3}m+\frac{1}{9}\right)-\frac{4}{3}\)
\(=3\left(m-\frac{1}{3}\right)^2-\frac{4}{3}\ge-\frac{4}{3}\)(do \(\left(m-\frac{1}{3}\right)^2\ge0\))
Thay vào A,ta có: \(A=\frac{3m^2-2m-1}{\left(m+1\right)^2}=\frac{3\left(m-\frac{1}{3}\right)^2-\frac{4}{3}}{\left(m+1\right)^2}\)
\(\ge\frac{\left(-\frac{4}{3}\right)}{\left(m+1\right)}=-\frac{4}{3\left(m+1\right)}=-\frac{4}{3m+3}\) (*)
Dấu "=" xảy ra khi \(m-\frac{1}{3}=0\Leftrightarrow m=\frac{1}{3}\)
Từ (*) suy ra \(\frac{1}{A}\ge-\frac{3m+3}{4}\ge-\frac{\frac{3.1}{3}+3}{4}=\frac{4}{4}=\frac{1}{1}\)
Suy ra \(A\ge\frac{1}{1}=1\)
Đúng 0
Bình luận (0)
X4-2.(m+2)x2+m2-2m+3=0
Định m để phương trình có 4 nghiệm
Tìm hệ thức độc lập với m
Tìm E=x1.x2.x3.x4 theo m .Tính GTNN của E
Đặt \(t=x^2\left(t\ge0\right)\)
Khi đó phương trình ban đầu tương đương với pt\(t^2-2\left(m+2\right)t+m^2-2m+3=0\) (*)
Để pt ban đầu có 4 nghiệm phân biệt thì pt (*) có hai nghiệm dương phân biệt ⇔
\(\left\{{}\begin{matrix}\Delta>0\\S>0\\P>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m+2\right)^2-m^2+2m-3>0\\2\left(m+2\right)>0\\m^2-2m+3>0\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}6m+1>0\\m+2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{6}\\m>-2\end{matrix}\right.\)
⇔ \(m>-\dfrac{1}{6}.\)
Giả sử (*) có hai nghiệm là t1, t2. Khi đó theo Viet ta có t1.t2 = m2 - 2m + 3.
Ta có: x1.x2.x3.x4 = t1.t2 = m2 - 2m +3.
Ta có E = m2 - 2m + 3 = (m - 1)2 + 2 ≥ 2.
Min E = 2. Dấu bằng xảy ra khi m = 1.
Đúng 1
Bình luận (0)
Tìm GTNN của biểu thức \(A=\frac{2m+7}{m^2+8}\)
tìm gtnn các biểu thức s a)x2+2x+2020
b)m2+4m-1
c)m2+m
d)x-2căn x+10
e)4x-8 căn x +2020
\(a,=x^2+2x+1+2019=\left(x+1\right)^2+2019\ge2019\) dấu"=" xảy ra<=>x=-1
b,\(=m^2+2.2m+4-5=\left(m+2\right)^2-5\ge-5\) dấu"=" xảy ra<=>m=-2
c, \(=x-2\sqrt{x}+10=x-2\sqrt{x}+1+9=\left(\sqrt{x}-1\right)^2+9\ge9\)
dấu"=" xảy ra<=>x=1
b, \(4x-8\sqrt{x}+2020=4x-2.2.2\sqrt{x}+4+2016=\left(2\sqrt{x}-2\right)^2+2016\ge2016\)
dấu"=" xảy ra<=>x=1
Đúng 1
Bình luận (0)
a) Ta có: \(x^2+2x+2020\)
\(=x^2+2x+1+2019\)
\(=\left(x+1\right)^2+2019\ge2019\forall x\)
Dấu '=' xảy ra khi x=-1
b) Ta có: \(m^2+4m-1\)
\(=m^2+4m+4-5\)
\(=\left(m+2\right)^2-5\ge-5\forall m\)
Dấu '=' xảy ra khi m=-2
c) Ta có: \(m^2+m\)
\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}\)
\(=\left(m+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\forall m\)
Dấu '=' xảy ra khi \(m=-\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
cho(m,n)=1. Tìm (A,B) với A=m+n . B= m^2+n^2
Giả sử: d=(m+n,m2+n2)
⇒ m+n ⋮ d và m^2+n^2 ⋮ d
⇒m^2+n^2+2mn ⋮ dvà m^2+n^2 ⋮ d
⇒2mn⋮ d và m+n ⋮ d
⇒2m(m+n) -2mn ⋮ d và 2n(m+n)−2mn ⋮ d
⇒2m^2 ⋮ d và 2n^2 ⋮ d
mình làm tới bước này rồi nhờ mọi người giải tiếp với với cách xét m,n cùng lẻ và m,n khác tính chẵn lẽ nhé 1