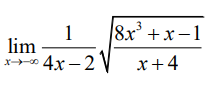a. Áp dụng công thức L'Hospital:

\(\lim\limits_{x\to 0}\frac{\sqrt{x+1}-\sqrt{1-x}}{\sqrt[3]{x+1}-\sqrt{1-x}}=\lim\limits_{x\to 0}\frac{\frac{1}{2}(x+1)^{\frac{-1}{2}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}{\frac{1}{3}(x+1)^{\frac{-2}{3}}+\frac{1}{2}(1-x)^{\frac{-1}{2}}}=\frac{1}{\frac{5}{6}}=\frac{6}{5}\)

b.

\(\lim\limits_{x\to 0}(\frac{1}{x}-\frac{1}{x^2})=\lim\limits_{x\to 0}\frac{x-1}{x^2}=-\infty\)

c. Áp dụng quy tắc L'Hospital:

\(\lim\limits_{x\to +\infty}\frac{x^4-x^3+11}{2x-7}=\lim\limits_{x\to +\infty}\frac{4x^3-3x^2}{2}=+\infty \)

d.

\(\lim\limits_{x\to 5}\frac{7}{(x-1)^2}.\frac{2x+1}{2x-3}=\frac{7}{(5-1)^2}.\frac{2.5+11}{2.5-3}=\frac{11}{16}\)

Lời giải:

\(\lim\limits_{x\to 5}\frac{2+\sqrt{x-4}-\sqrt{x+4}}{x-5}=\lim\limits_{x\to 5}\frac{(\sqrt{x-4}-1)-(\sqrt{x+4}-3)}{x-5}=\lim\limits_{x\to 5}\frac{\frac{x-5}{\sqrt{x-4}+1}-\frac{x-5}{\sqrt{x+4}+3}}{x-5}\)

\(=\lim\limits_{x\to 5}\left(\frac{1}{\sqrt{x-4}+1}-\frac{1}{\sqrt{x+4}+3}\right)=\frac{1}{3}\)

a/ \(=\lim\limits_{x\rightarrow\pm\infty}\dfrac{\dfrac{\left(2x\right)^2.\left(4x\right)^3}{x^4}}{\dfrac{\left(3x\right)^2\left(5x^2\right)}{x^4}}=\lim\limits_{x\rightarrow\pm\infty}\dfrac{4^4.x}{45}=\pm\infty\)

b/ \(=\lim\limits_{x\rightarrow\pm\infty}\dfrac{\sqrt[3]{\dfrac{x^3}{x^3}+\dfrac{2x^2}{x^3}+\dfrac{x}{x^3}}}{\dfrac{2x}{x}-\dfrac{2}{x}}=\dfrac{1}{2}\)

c/ \(=\lim\limits_{x\rightarrow\pm\infty}\dfrac{\dfrac{\sqrt[3]{\left(x^3+2x^2\right)^2}}{x^2}+\dfrac{x\sqrt[3]{x^3+2x^2}}{x^2}+\dfrac{x^2}{x^2}}{\dfrac{3x^2}{x^2}-\dfrac{2x}{x^2}}=\dfrac{1+1+1}{3}=1\)

d/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{\left(-3x\right)^3x^2}{x^5}}{-\dfrac{4x^5}{x^5}}=\dfrac{-27}{-4}=\dfrac{27}{4}\)

e/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{\left(2x\right)^{20}.\left(3x\right)^{20}}{x^{50}}}{\dfrac{\left(2x\right)^{50}}{x^{50}}}=0\)

g/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{8x^3.\left(4x^5\right)^9}{x^{47}}}{\dfrac{11x^{47}}{x^{47}}}=+\infty\)

giúp mình với mn ơi

\(\lim\limits_{x\rightarrow\infty}\left(\sqrt{x+1}-\sqrt{x}\right)=\lim\limits_{x\rightarrow\infty}\dfrac{1}{\sqrt{x+1}+\sqrt{x}}=\dfrac{1}{\infty}=0\).

a) \(lim_{x\rightarrow+\infty}\left(\sqrt{x+1}-\sqrt{x}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{1}{\sqrt{x+1}+\sqrt{x}}\right)=0\)

b) \(lim_{x\rightarrow+\infty}\left(\sqrt{x+\sqrt{x}}-\sqrt{x}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{x+\sqrt{x}-x}{\sqrt{x+\sqrt{x}}+\sqrt{x}}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{\sqrt{x}}{\sqrt{x+\sqrt{x}}+\sqrt{x}}\right)\)

\(=lim_{x\rightarrow+\infty}\left(\dfrac{1}{\sqrt{\dfrac{x+\sqrt{x}}{x}}+1}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{1}{\sqrt{1+\dfrac{1}{\sqrt{x}}}+1}\right)=\dfrac{1}{2}\)

c) \(lim_{x\rightarrow-\infty}\left(\sqrt{3x^2+x+1}+x\sqrt{3}\right)=lim_{x\rightarrow-\infty}\left(\dfrac{x+1}{\sqrt{3x^2+x+1}-x\sqrt{3}}\right)\)

\(=lim_{x\rightarrow-\infty}\left(\dfrac{1+\dfrac{1}{x}}{\sqrt{\dfrac{3x^2+x+1}{x^2}}-\dfrac{x\sqrt{3}}{x^2}}\right)\)

\(=lim_{x\rightarrow-\infty}\left(\dfrac{1+\dfrac{1}{x}}{\sqrt{3+\dfrac{1}{x}+\dfrac{1}{x^2}}-\dfrac{\sqrt{3}}{x}}\right)=\dfrac{1}{\sqrt{3}}\)

d) \(lim_{x\rightarrow+\infty}\left(\sqrt{x^2+2x+4}-\sqrt{x^2-2x+4}\right)=lim_{x\rightarrow+\infty}\left(\dfrac{4x}{\sqrt{x^2+2x+4}+\sqrt{x^2-2x+4}}\right)\)

\(=lim_{x\rightarrow+\infty}\left(\dfrac{4}{\sqrt{1+\dfrac{2}{x}+\dfrac{4}{x^2}}+\sqrt{1-\dfrac{2}{x}+\dfrac{4}{x^2}}}\right)=\dfrac{4}{2}=2\)

\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+\sqrt{x^2+2}}{\sqrt{8x^2+5x+2}}=\dfrac{1+\sqrt{1+\dfrac{2}{x^2}}}{\sqrt{8+\dfrac{5}{x}+\dfrac{2}{x^2}}}=\dfrac{1+\sqrt{1}}{\sqrt{8}}=\dfrac{\sqrt{2}}{2}\).

3.

Đặt \(f\left(x\right)=x^4-3x^3+x-\dfrac{1}{8}\)

Hàm \(f\left(x\right)\) liên tục trên R

Do \(f\left(x\right)\) là đa thức bậc 4 nên có tối đa 4 nghiệm

Ta có: \(f\left(-1\right)=\dfrac{23}{8}>0\)

\(f\left(0\right)=-\dfrac{1}{8}< 0\Rightarrow f\left(-1\right).f\left(0\right)< 0\)

\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)

\(f\left(\dfrac{1}{2}\right)=\dfrac{1}{16}>0\Rightarrow f\left(0\right).f\left(\dfrac{1}{2}\right)< 0\)

\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\dfrac{1}{2}\right)\)

\(f\left(1\right)=-\dfrac{9}{8}< 0\Rightarrow f\left(\dfrac{1}{2}\right).f\left(1\right)< 0\)

\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(\dfrac{1}{2};1\right)\)

\(f\left(3\right)=\dfrac{23}{8}>0\Rightarrow f\left(1\right).f\left(3\right)< 0\)

\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;3\right)\)

Vậy pt có 4 nghiệm thuộc các khoảng nói trên

4.

\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+ax+2017}+x\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{ax+2017}{\sqrt{x^2+ax+2017}-x}\)

\(=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{2017}{x}}{-\sqrt{1+\dfrac{a}{x}+\dfrac{2017}{x^2}}-1}=-\dfrac{a}{2}\)

\(\Rightarrow-\dfrac{a}{2}=6\Rightarrow a=-12\)

\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4+2x}-\sqrt[3]{8-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{4+2x}-2}{x}+\lim\limits_{x\rightarrow0}\dfrac{2-\sqrt[3]{8-x}}{x}\)

\(=\lim\limits_{x\rightarrow0}\dfrac{4+2x-4}{x\left(\sqrt{4+2x}+2\right)}+\lim\limits_{x\rightarrow0}\dfrac{8-8+x}{x\left(\sqrt[3]{\left(8-x\right)^2}+2.\sqrt[3]{8-x}+4\right)}\)

\(=\dfrac{2}{\sqrt{4}+2}+\dfrac{1}{\sqrt[3]{8^2}+2.\sqrt[3]{8}+4}=\dfrac{7}{12}\)