Mình quên còn ý b . Trên tia đối của tia AC lấy điểm M sao cho AM =AB.Trên tia đối của tia CA lấy điểm N sao  cho BC=CN. CM BN>BM

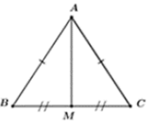
Δ A B C  cân tại A (gt)  mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó.

Vì AM  là trung tuyến của  Δ A B C nên M là trung điểm của BC

⇒ B M = B C 2 = 24 : 2 = 12 c m

a/ kéo dài đoạn thẳng BG cắt AC tại D.Vì 3 đường trung tuyến cùng đi qua 1 điểm nên BD là đường trung truyến của góc B.

b/ Vì tam giác ABc vuông tại A nên góc C là góc nhọn suy ra góc BCN là góc tù suy ra góc CNB là góc nhọn suy ra BN> CN

vậy BA<CN<BN

 BẠN TỰ VẼ HÌNH ĐI NHÉ.... NẾU THẤY ĐÚNG THÌ K CHO MÌNH VỚI

a) Xét ΔABD và ΔACD có 

AB=AC(ΔABC cân tại A)

\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))

AD chung

Do đó: ΔABD=ΔACD(c-g-c)

Suy ra: BD=CD(hai cạnh tương ứng)

mà B,D,C thẳng hàng(gt)

nên D là trung điểm của BC

Xét ΔABC có 

AD là đường trung tuyến ứng với cạnh BC(cmt)

BE là đường trung tuyến ứng với cạnh BC(gt)

AD cắt BE tại O(gt)

Do đó: O là trọng tâm của ΔABC(Định lí ba đường trung tuyến của tam giác)

b) Ta có: D là trung điểm của BC(cmt)

nên \(BD=CD=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)

Ta có: ΔABD=ΔACD(cmt)

nên \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)

mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)

nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)

Áp dụng định lí Pytago vào ΔABD vuông tại D, ta được:

\(AB^2=AD^2+BD^2\)

\(\Leftrightarrow AD^2=5^2-4^2=25-16=9\)

hay AD=3(cm)

Xét ΔABC có 

AD là đường trung tuyến ứng với cạnh CB(cmt)

O là trọng tâm của ΔABC(cmt)

Do đó: \(OD=\dfrac{1}{3}AD\)(Tính chất trọng tâm của tam giác)

hay OD=1(cm)

Vậy: OD=1cm

c) Xét ΔABC có 

O là giao điểm của 3 đường phân giác

O là giao điểm của 3 đường trung tuyến

Do đó: ΔABC đều

a: Xét ΔABC vuông tạiA và ΔAEC vuông tại A có

AB=AE

AC chung

=>ΔABC=ΔAEC

b: Xet ΔCEB có

CA,BH là trung tuyến
CA cắt BH tại M

=>M là trọng tâm

=>CM=2/3*12=8cm

c: Xét ΔCBE có

A là trung điểm của BE

AK//CE
=>K la trung điểm của BC

=>E,M,K thẳng hàng