Giải tự luận giúp mink với

ai có đề cương các môn học lớp 7 bình luận ở dưới giúp mink, mink sắp thi học kì 1 đang cần gấp các bạn giúp mink với nha!!!! mink cảm ơn nhiều
mn giải giúp mink với mink cần rất gấp
(-4) x y -5=23-32
mn x là nhân nha,mn giúp mink với nhá.Thank you mn thân thương
![]()
Giải giúp em 13,14,15,16 tự luận với ạ
Giải giúp mk phần tự luận với ạ
1. Đề lỗi
2.
Đường tròn (C) tâm \(I\left(1;-1\right)\) bán kính \(R=\sqrt{1^2+\left(-1\right)^2-\left(-7\right)}=3\)
a.
\(d\left(I;D\right)=\dfrac{\left|1-1-4\right|}{\sqrt{1^2+1^2}}=2\sqrt{2}< R\)
\(\Rightarrow D\) cắt (C) tại 2 điểm phân biệt
b.
Gọi H là trung điểm MN \(\Rightarrow IH\perp MN\Rightarrow IH=d\left(I;D\right)=2\sqrt{2}\)
ÁP dụng định lý Pitago trong tam giác vuông IHM:
\(HM=\sqrt{IM^2-IH^2}=\sqrt{R^2-IH^2}=\sqrt{9-8}=1\)
\(\Rightarrow MN=2MH=2\)
\(S_{IMN}=\dfrac{1}{2}IH.MN=2\sqrt{2}\)
3.
Đường tròn (C) tâm \(I\left(2;3\right)\) bán kính \(R=\sqrt{2}\)
Đường còn (C') tâm \(I'\left(1;2\right)\) bán kính \(R'=2\sqrt{2}\)
Gọi tiếp tuyến chung của (C) và (C') là (d) có pt: \(ax+by+c=0\) với \(a^2+b^2\ne0\)
\(\Rightarrow\left\{{}\begin{matrix}d\left(I;\left(d\right)\right)=R\\d\left(I';\left(d\right)\right)=R'\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{\left|2a+3b+c\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\left(1\right)\\\dfrac{\left|a+2b+c\right|}{\sqrt{a^2+b^2}}=2\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow\left|a+2b+c\right|=2\left|2a+3b+c\right|\)
\(\Rightarrow\left[{}\begin{matrix}4a+6b+2c=a+2b+c\\4a+6b+2c=-a-2b-c\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3a+4b+c=0\\5a+8b+3c=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}c=-3a-4b\\c=-\dfrac{5a+8b}{3}\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow\left[{}\begin{matrix}\dfrac{\left|2a+3b-3a-4b\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\\\dfrac{\left|2a+3b-\dfrac{5a+8b}{3}\right|}{\sqrt{a^2+b^2}}=\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left|a+b\right|=\sqrt{2\left(a^2+b^2\right)}\\\left|a+b\right|=3\sqrt{2\left(a^2+b^2\right)}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a^2+2ab+b^2=2a^2+2b^2\\a^2+2ab+b^2=18a^2+18b^2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(a-b\right)^2=0\\17a^2-2ab+17b^2=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow a=b\) \(\Rightarrow c=-3a-4b=-7a\)
Thế vào pt (d):
\(ax+ay-7a=0\Leftrightarrow x+y-7=0\)
4.
ĐKXĐ: \(x\ge-\dfrac{3}{2}\)
\(4\left(x+1\right)^2< \left(x+10\right)\left(1-\sqrt{3+2x}\right)^2\)
\(\Leftrightarrow4\left(x+1\right)^2< \left(x+10\right)\left(\dfrac{-2-2x}{1+\sqrt{3+2x}}\right)^2\)
\(\Leftrightarrow4\left(x+1\right)^2< \dfrac{\left(x+10\right)4\left(x+1\right)^2}{\left(1+\sqrt{3+2x}\right)^2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\\dfrac{x+10}{\left(1+\sqrt{3+2x}\right)^2}>1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\x+10>1+3+2x+2\sqrt{3+2x}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\6-x>2\sqrt{3+2x}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\6-x>0\\\left(6-x\right)^2>4\left(3+2x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\x< 6\\x^2-20x+24>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ne-1\\x< 10-2\sqrt{19}\end{matrix}\right.\)
Kết hợp ĐKXĐ ta được nghiệm của BPT là:
\(\left[{}\begin{matrix}-\dfrac{3}{2}\le x< -1\\-1< x< 10-2\sqrt{19}\end{matrix}\right.\)
(giải giúp mink bài này với mink đga cần gấp) 
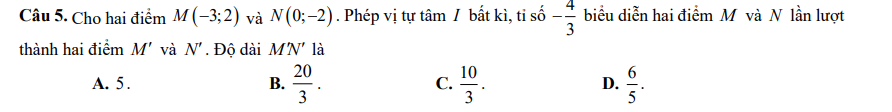
giải giúp em theo phương pháp tự luận với
MN = \(\sqrt{\left(-3-0\right)^2+\left(2+2\right)^2}=5\)
Phép vị tự tâm I biến M và N thành M' và N' với tỉ số vị tự là \(-\dfrac{4}{3}\)
⇒ \(\overrightarrow{M'N'}=-\dfrac{4}{3}\overrightarrow{MN}\)
⇒ M'N' = \(\dfrac{4}{3}.MN=\dfrac{4}{3}.5=\dfrac{20}{3}\) (đơn vị độ dài)
Giải giúp mình hết phần tự luận với ạ
giải giúp em câu 3,4 tự luận với ạ
Câu 3:
\(n_{CO_2}=\dfrac{0,44}{44}=0,01\left(mol\right)\)
\(n_{H_2O}=\dfrac{0,18}{18}=0,01\left(mol\right)\)
Bảo toàn C: nC(A) = 0,01 (mol)
Bảo toàn H: nC(A) = 2.0,01 = 0,02 (mol)
=> \(n_O=\dfrac{0,3-0,01.12-0,02.1}{16}=0,01\left(mol\right)\)
nC : nH : nO = 0,01 : 0,02 : 0,01 = 1:2:1
=> CTHH: (CH2O)n
Có\(n_{O_2}=\dfrac{0,32}{32}=0,01\left(mol\right)=>M_A=\dfrac{0,3}{0,01}=30\left(g/mol\right)\)
=> n = 1
=> CTHH: CH2O
Câu 4:
\(n_{NO_2}=\dfrac{5,152}{22,4}=0,23\left(mol\right)\)
PTHH: Cu + 4HNO3 --> Cu(NO3)2 + 2NO2 + 2H2O
_____a---------------------------------->2a
Fe + 6HNO3 --> Fe(NO3)3 + 3NO2 + 3H2O
b---------------------------------->3b
=> \(\left\{{}\begin{matrix}64a+56b=5,36\\2a+3b=0,23\end{matrix}\right.=>\left\{{}\begin{matrix}a=0,04\\b=0,05\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}\%Cu=\dfrac{0,04.64}{5,36}.100\%=47,76\%\\\%Fe=\dfrac{0,05.56}{5,36}.100\%=52,24\%\end{matrix}\right.\)
Giải giúp mình phần tự luận với ạ🥺
Câu 5:
$\frac{20}{\sqrt{5}}=\frac{20\sqrt{5}}{5}=4\sqrt{5}$
Câu 6:
\(\frac{3}{\sqrt{5}+\sqrt{2}}+\frac{3}{\sqrt{5}-\sqrt{2}}=3.\frac{\sqrt{5}-\sqrt{2}+\sqrt{5}+\sqrt{2}}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}=3.\frac{2\sqrt{5}}{5-2}=2\sqrt{5}\)
Câu 7:
1. ĐKXĐ: $x\neq 1; x\geq 0$
\(A=\left[\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+1}+1\right]:\left[\frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}-1}-1\right]=(\sqrt{x}+1):(\sqrt{x}-1)\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
2.
\(A< 1\Leftrightarrow \frac{\sqrt{x}+1}{\sqrt{x}-1}-1<0\Leftrightarrow \frac{2}{\sqrt{x}-1}<0\)
\(\Leftrightarrow \sqrt{x}-1<0\Leftrightarrow x< 1\)
Kết hợp ĐKXĐ suy ra $0\leq x< 1$