Cho phân số \(\frac{3}{-7}=\frac{a}{b}\)
a, Tìm phân số \(\frac{c}{d};\frac{e}{g}=\frac{a}{b}\)có mẫu theo thứ tự là 35 và -42
b, Tìm phân số = \(\frac{a}{b}\)có tổng của tử và mẫu bằng -8
Trong các phân số sau đây, tìm phân số không bằng phân số nào trong các phân số còn lại
\(a.\frac{-7}{33}b.\frac{12}{18}c.\frac{3}{-18}d.\frac{-9}{54}e.\frac{-10}{-15}f.\frac{14}{20}\)
Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 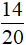
Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 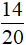
Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 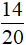
Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 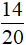
Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 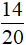
Tìm số đối của mỗi phân số sau (có dùng kí hiệu số đối của phân số).
a) \(\frac{{ - 15}}{7}\) b) \(\frac{{22}}{{ - 25}}\)
c) \(\frac{{10}}{9}\) d) \(\frac{{ - 45}}{{ - 27}}\)
a) Số đối của \(\frac{{ - 15}}{7}\) là \(\frac{{15}}{7}\)
b) Số đối của \(\frac{{22}}{{ - 25}}\) là \(\frac{{22}}{{25}}\)
c) Số đối của \(\frac{{10}}{9}\) là \(\frac{{ - 10}}{9}\)
d) Số đối của\(\frac{{ - 45}}{{ - 27}}\) là \(\frac{{ - 45}}{{27}}\).
CHO PHÂN SỐ \(\frac{a}{b}\)khác 1
tìm phân số \(\frac{c}{d}\)sao cho \(\frac{a}{b}+\frac{c}{d}=\frac{a}{b}.\frac{c}{d}\)
\(\frac{a}{b}+\frac{c}{d}=\frac{a.c}{b.d}\)
Vậy \(\frac{a.d+b.c}{bd}=\frac{ac}{bd}\)
\(\Leftrightarrow ad+bc=ac\)
\(\Leftrightarrow ad=ac-bc\)
\(\Leftrightarrow ad=c\left(a-b\right)\)
\(\Leftrightarrow\frac{a}{b}=\frac{a}{a-b}\)
\(\frac{a}{b}+\frac{c}{d}=\frac{a\cdot c}{b\cdot d}\)
Vậy \(\frac{a\cdot b+b\cdot c}{bd}=\frac{ac}{bd}\)
\(\Rightarrow ad+bc=ac\)
\(\Rightarrow ad=ac-bc\)
\(\Rightarrow ad=c\left(a-b\right)\)
\(\Rightarrow\frac{a}{b}=\frac{a}{a-b}\)
Bài 1 ; Tìm 3 phân số có mẫu khác nhau , các phân số này lớn hơn \(\frac{1}{4}\)và nhỏ hơn \(\frac{1}{3}\)
Bài 2 : Cho các số a,b ,c,d.Chứng minh rằng :
\(1< \frac{a}{a+c+c}+\frac{b}{b+c+d}+\frac{c}{c+d+a}+\frac{d}{d+a+b}< 2\)
Bài 1 :
Từ \(\frac{1}{4}< \frac{1}{3}\) suy ra \(\frac{1}{4}< \frac{1+1}{4+3}< \frac{1}{3}\) hay \(\frac{1}{4}< \frac{2}{7}< \frac{1}{3}\)
Từ \(\frac{1}{4}< \frac{2}{7}\)suy ra \(\frac{1}{4}< \frac{1+2}{4+7}< \frac{1}{3}\)hay \(\frac{1}{4}< \frac{3}{11}< \frac{1}{3}\)
Từ \(\frac{2}{7}< \frac{1}{3}\)suy ra \(\frac{2}{7}< \frac{2+1}{7+3}< \frac{1}{3}\)hay \(\frac{2}{7}< \frac{3}{10}< \frac{1}{3}\)
Vậy ta có : \(\frac{1}{4}< \frac{3}{11}< \frac{2}{7}< \frac{3}{10}< \frac{1}{3}\)
Chúc bạn học tốt ( -_- )
Bài 2 :
\(\frac{a}{a+b+c+d}< \frac{a}{a+b+c}< \frac{a}{a+c}\left(1\right)\)
\(\frac{b}{a+b+c+d}< \frac{b}{b+c+d}< \frac{b}{b+d}\left(2\right)\)
\(\frac{c}{a+b+c+d}< \frac{c}{c+d+a}< \frac{c}{c+a}\left(3\right)\)
\(\frac{d}{a+b+c+d}< \frac{d}{d+a+b}< \frac{d}{d+b}\left(4\right)\)
Cộng ( 1 ), ( 2 ) , (3 ) và ( 4 ) theo từng vế ta được :
\(1=\frac{a+b+c+d}{a+b+c+d}< \frac{a}{a+b+c}+\frac{b}{b+c+d}\)\(+\frac{c}{c+d+a}+\frac{d}{d+a+b}< \frac{a+c}{a+c}+\frac{b+d}{b+d}\)
Chúc bạn học tốt ( -_- )
Cho phân số \(\frac{a}{b}\),rút gọn phân số ta được phân số \(\frac{3}{7}\).Nếu thêm 7 đơn vị vào mẫu số b mà giữ nguyên tử số a thì ta được một phân số mới.Rút gọn phân số mới ta được phân số \(\frac{3}{8}\).Tìm phân số \(\frac{a}{b}\)
Cho phân số \(\frac{a}{b}\) .Rút gọn phân số \(\frac{a}{b}\) ta được phân số \(\frac{5}{14}\) Nếu bớt 7 đơn vị ở mẫu số và giữ nguyên tử số ta được phân số mới .Rút gon phân số mới ta được phân số \(\frac{3}{7}\) .Tìm phân số \(\frac{a}{b}\) .
ta có \(\hept{\begin{cases}\frac{a}{b}=\frac{5}{14}\\\frac{a}{b-7}=\frac{3}{7}\end{cases}\Rightarrow\hept{\begin{cases}14a=5b\\7a=3\left(b-7\right)\end{cases}\Rightarrow}\hept{\begin{cases}a=\frac{5b}{14}\\7\left(\frac{5b}{14}\right)-3\left(b-7\right)=0\end{cases}}\Rightarrow\hept{\begin{cases}a=\frac{5b}{14}\\\frac{5b}{2}-3b+21=0\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}a=\frac{5b}{14}\\5b-6b+42=0\end{cases}\Rightarrow\hept{\begin{cases}a=\frac{5b}{14}\\-b=-42\end{cases}}\Rightarrow\hept{\begin{cases}a=\frac{5b}{14}\\b=42\end{cases}\Rightarrow}\hept{\begin{cases}a=\frac{5\cdot42}{14}\\b=42\end{cases}}\Rightarrow\hept{\begin{cases}a=15\\b=42\end{cases}}}\)
Vậy phân số \(\frac{a}{b}=\frac{15}{42}\)
Bài 1: a, Tìm số nguyên a để tích hai phân số \(\frac{-19}{5}\) và \(\frac{a}{a-1}\)là một số nguyên.
b, Tìm số nguyên a để \(\frac{5}{4}\): \(\frac{a}{a+1}\)được thương là một số nguyên.
c,Tìm phân số dương \(\frac{a}{b}\)nhỏ nhất sao cho khi chia \(\frac{a}{b}cho\frac{7}{9}\)hoặc khi chia cho \(\frac{5}{12}\)được mỗi thương là một số tự nhiên
Bài 2:a,Với giá trị nào của x thì ta có:
1,A= \(\left(x-\frac{3}{4}\right)\left(x+\frac{1}{2}\right)\)là số dương 2,B=\(\frac{x-0,5}{x+1}\)là số âm.
b,Cho phân số \(\frac{a}{b}\left(b\ne0\right)\).Tìm phân số \(\frac{c}{d}\left(c\ne0,d\ne0\right)\)sao cho \(\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{c}{d}\)
c, Tìm các cặp số nguyên (x,y) để: \(B=\frac{1}{x-y}:\frac{x+2}{2\left(x-y\right)}\)là số nguyên.
Bài 3: a, Tính : A=\(\left(-2\right)\left(-1\frac{1}{2}\right)\left(-1\frac{1}{3}\right)\left(-1\frac{1}{4}\right)...\left(-1\frac{1}{n}\right)\left(n\in N,n\ne0\right)\)
B=\(\frac{4\frac{1}{4}}{11\frac{1}{3}.5\frac{1}{4}}\) C= \(\frac{-1:1\frac{1}{15}}{3\frac{1}{8}:6\frac{2}{3}}:\frac{4\frac{7}{8}:13}{5:1\frac{7}{8}}\) D=\(-\frac{7}{4}\left(\frac{33}{12}+\frac{3333}{2020}+\frac{333333}{303030}+\frac{33333333}{42424242}\right)\)
E=\(\frac{1}{2}:\left(-1\frac{1}{2}\right):1\frac{1}{3}:\left(-1\frac{1}{4}\right):1\frac{1}{5}:\left(-1\frac{1}{6}\right):...:\left(-1\frac{1}{100}\right)\) F=\(4+\frac{1}{1+\frac{1}{1+\frac{2}{1+\frac{3}{4}}}}\)
nhiều thế ??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
Viết phân số sau ở dạng tổng các phân số có mẫu số là số tự nhiên khác nhau nhưng có cùng tử số là 1.
a) \(\frac{2}{3}\); b)\(\frac{8}{{15}}\)
c) \(\frac{7}{8}\); d) \(\frac{{17}}{{18}}\).
Gợi ý:
a) \(\frac{2}{3} = \frac{1}{2} + ?;\)
c) \(\frac{7}{8} = \frac{1}{2} + ? + ?;\)
a) \(\frac{2}{3} = \frac{4}{6} = \frac{1}{6} + \frac{3}{6} = \frac{1}{6} + \frac{1}{2}\)
b) \(\frac{8}{{15}} = \frac{5}{{15}} + \frac{3}{{15}} = \frac{1}{5} + \frac{1}{3}\)
c) \(\frac{7}{8} = \frac{4}{8} + \frac{2}{8} + \frac{1}{8} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8}\)
d) \(\frac{{17}}{{18}} = \frac{9}{{18}} + \frac{6}{{18}} + \frac{2}{{18}} = \frac{1}{2} + \frac{1}{3} + \frac{1}{9}\).
Cho hai phan số \(\frac{6}{7}\) và\(\frac{1}{9}\) . Tìm phân số \(\frac{a}{b}\)sao cho khi thêm vào \(\frac{a}{b}\) vào phân số \(\frac{1}{9}\) và bớt\(\frac{a}{b}\) ở phân số \(\frac{6}{7}\) ta được hai phân số có tỉ số là 3.