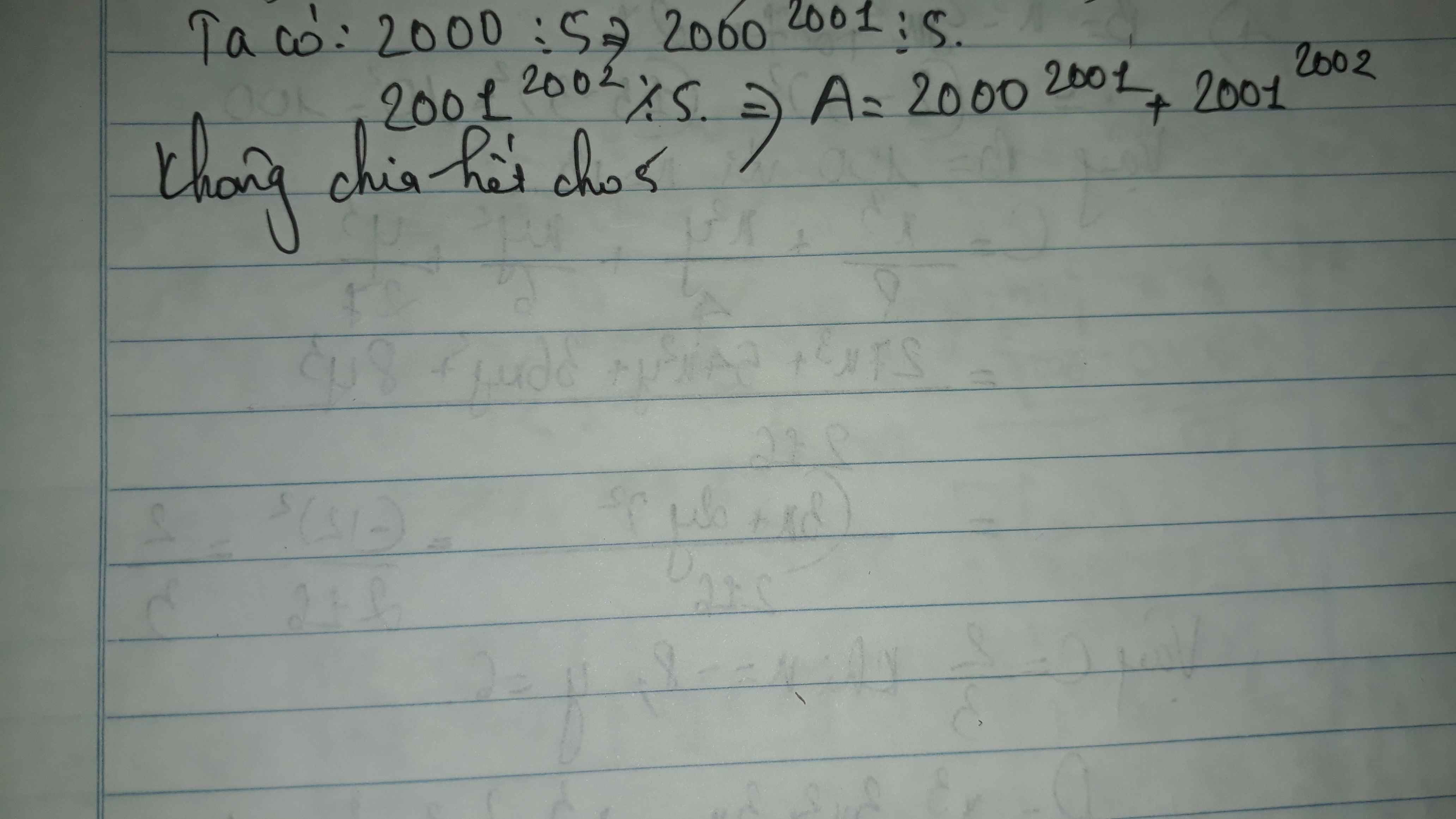CTR:
a/ 20012002 + 20023 ko chia hết cho 2
b/ 8617 + 9722 chia hết cho 5

Những câu hỏi liên quan
Không làm phép tính, hãy cho biết các số sau có chia hết cho 5 không ?
A = 20002001+ 20012002
\(2000^{2001}⋮5\)
mà \(2001^{2002}⋮̸5\)
nên \(A⋮̸5\)
Đúng 0
Bình luận (0)
cho (a + 3b) chia hết cho 5 hỏi (4a + 2b) có chia hết cho 5 ko
dm câu nữa nha cho (a + 3b) chia hết cho 5 hỏi (4a + 2b) có chia hết cho 5 ko
bài 7:tìm điều kiện cửa số x e N de:
a=12+14+16+x chia hết cho 2;ko chia hết cho 2
a=8+12+x chia hết cho 4;ko chia hết cho 4
a=6+12+27+x chia hết cho 3 ko chia hết cho 3
a=5+70+x chia hết cho 5;ko chia hết 5;chia hết cho 10;ko chia hết cho 10
a=10+15+20+x chia hết cho 5;ko chia hết cho 5.
12 + 14 + 16 + x chia hết cho 2
12 ; 14 ; 16 chia hết cho 2 => x chia hết cho 2
12 + 14 + 16 không chia hết cho 2
12 ; 14 ; 16 chia hết cho 2 => x không chia hết cho 2 (lẻ)
Đúng 0
Bình luận (0)
Tìm điều kiện của số x thuộc stn để :
a)A=12+14+16+x chia hết cho 2 ;ko chia hết cho 2
b)A=8+12+x chia hết cho 4 và ko chia hết cho 4
c)A=6+12+27+x chia hết cho3 và ko chia hết cho 3
d)A=5+70+x chia hết cho 5;ko chia hết cho 5 ,chia hết cho 10 và ko chia hết cho 10
e)A=10+15+20+x chia hết cho 5 và ko chia hết cho 5
a ) Để A chia hết cho 2 ; x là số chẵn
Để A không chia hết cho 2 ; x là số lẻ
b ) Để A chia hết cho 4 ; x chia hết cho 4
Để A khộng chia hết cho 4 thì ngược lại
c ) Để A không chia hết cho 3 ; x không chia hết cho 3
Để A chia hét cho 3 ; x phải chia hết cho 3
Đúng 2
Bình luận (0)
chứng minh rằng
a) nếu 20a + 11b chia hết cho 17 thì 83a + 38b chia hết cho17
b) nếu (2a +3b +4c) chia hết cho 7 thì ( 13a + 2b - 2c ) chia hết cho 7
c) nếu a +4b chia hết cho 13 thì 10a + b chia hết cho 13
d) nếu a + 2b chia hết cho 5 thì 3a - 4b chia hết cho 5
e) nếu a - 5b chia hết cho 17 thì 10a + b chia hết cho 17
Câu trả lời hay nhất: + ta chứng minh a,b,c có ít nhất một số chia hết cho 3
giả sử cả 3 số trên đều không chia hết cho 3
=> a^2 = 1 (mod3) và b^2 = 1 (mod3) (bình phương 1 số chia hết cho 3 hoạc chia 3 dư 1)
=> a^2 + b^2 = 2 (mod3) nhưng c^2 = 1 (mod3) => mâu thuẫn
Vậy có ít nhất 1 số chia hết cho 3
+ tương tự,có ít nhất 1 số chia hết cho 4,vì giả sử cả 3 số a,b,c đều không chia hết cho 4
=> a^2 = 1 (mod4) và b^2 = 1 (mod4) => a^2 + b^2 = 2 (mod 4) nhưng c^2 = 1 (mod 4) => mâu thuẫn
vậy có ít nhất 1 số cgia hết cho 4
+ tương tự a^2 = 1 (mod 5) hoạc a^2 = -1 (mod 5) hoạc a^2 = 4 (mod 5)
và -1 + 1 = 0,1 + 4 = 5,-1 + 4 = 3
=> phải có ít nhất 1 số chia hết cho 5
Vậy abc chia hết cho BCNN(3,4,5) = 60 hay abc chia hết 60
Đúng 0
Bình luận (0)
a+5b ⋮ 7
=> 3(a+5b) ⋮7
=> 3a+15b⋮7
=> 3a+15b +7a -14b⋮7
=> 10a+b⋮7
chúc bn hok tốt ^_^
Đúng 0
Bình luận (0)
Ta có : 83a + 38b chia hết cho 17
Suy ra : 17a +83a + 38b + 17b chia hết cho 17
Suy ra 100a +55b chia hết cho 17
Suy ra 5×(20a +11b ) chia hết cho 17
Suy ra 20a +11b chia hết cho 17 ( do5 không chia hết cho 17)
Vậy 83a +38b chia hết cho 17 thì 20a +17b chia hết cho 17
Đúng 0
Bình luận (0)
Cho A=1+2+2^2+2^3+...+2^2013+2^2014 a,Tính A b,CTR:A chia hết cho 31
a,A = 1 + 2 + 22 + 23 +.... + 22013 + 22014
2A = 2 + 22 + 23 + ...... + 22013 + 22014 + 22015
A = ( 2 + 22 + 23 + ..... + 22013 + 22014 + 22015 ) - ( 1 + 2 + 22 + 23 + ..... + 22013 + 22014 )
A = 22015 - 1
b, A = 1 + 2 + 22 + 23 + ... + 22013 + 22014
= ( 1 + 2 + 22 + 23 + 24 ) + .... + ( 22010 + 22011 + 22012 + 22013 + 22014 )
= 31 + ..... + 22010.( 1 + 2 + 22 + 23 + 24 )
= 31 + ..... + 22010 . 31
= 31.1 + ..... + 22010 . 31
= 31. ( 1 + .... + 22010 ) chia hết cho 31
=> A chia hết cho 31
Đúng 0
Bình luận (0)
a) \(A=1+2+2^2+2^3+....+2^{2014}\)
\(\Leftrightarrow\)\(2A=2+2^2+2^3+2^4+...+2^{2015}\)
\(\Leftrightarrow\)\(2A-A=\left(2+2^2+2^3+...+2^{2015}\right)-\left(1+2+2^2+...+2^{2014}\right)\)
\(\Leftrightarrow\)\(A=2^{2015}-1\)
b) \(A=1+2+2^2+2^3+...+2^{2014}\)
\(=\left(1+2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8+2^9\right)\)\(+...+\left(2^{2010}+2^{2011}+2^{2012}+2^{2013}+2^{2014}\right)\)
\(=\left(1+2+2^2+2^3+2^4\right)+2^5\left(1+2+2^2+2^3+2^4\right)\)\(+...+2^{2010}\left(1+2+2^2+2^3+2^4\right)\)
\(=\left(1+2+2^2+2^3+2^4\right)\left(1+2^5+...+2^{2010}\right)\)
\(=31\left(1+2^5+...+2^{2010}\right)\) \(⋮31\)
Đúng 0
Bình luận (0)
a; A = 1 + 2+ 22 + 23 +..................+ 22013 + 22014
2A = 2+ 22 + 23 +..................+ 22013 + 22015
2A - A = [ 2+ 22 + 23 +..................+ 22013 + 22015 ] - [ 1 + 2+ 22 + 23 +..................+ 22013 + 22014 ]
A = 22015 - 1
b; A= 1 + 2+ 22 + 23 +..................+ 22013 + 22014
A = [ 1 + 2+ 22 + 23 ] + [ 24 + 25 + 26 + 27 ] +[ 28+29+210+211 ]+..................+ [ 22011+ 22012+22013+ 22014 ]
A = 31 + 23 [1 + 2 +22 + 23 + 24 ] + 28 [ 1 + 2+ 22 + 23 ] + ................+ 22011 [ 1 + 2+ 22 + 23 ]
A = 31 + 23 .31 + 28 . 31 +....................+ 22011 . 31
A = 31 [ 23 + 28 +..........+ 22011 ]
Mà 31 chia hết cho 31 => 31 [ 23 + 28 +..........+ 22011 ] chia hết cho 31 hay A chia hết cho 31
Vậy bài toán được chứng minh
Đúng 0
Bình luận (0)
cho a-b chia hết cho 5. Chứng minh rằng:
a - 6b chia hết cho 52b - 7b chia hết cho 526a - 21b + 2000 chia hết cho 5+ a - b chia hết cho 5
Mà 5b chia hết cho 5
=> a - b - 5b chia hết cho 5
=> a - 6b chia hết cho 5
Đúng 0
Bình luận (0)
+) a - b chia hết cho 5 => 2a - 2b chia hết cho 5
Mà 5b chia hết cho 5
=> 2a - 2b - 5b chia hết cho 5
=> 2a - 7b chia hết cho 5
Đúng 0
Bình luận (0)
+) a - b chia hết cho 5 => 21a - 21b chia hết cho 5
Mà 5a chia hết cho 5; 2000 chia hết cho 5
=> 21a + 5a - 21b + 2000 chia hết cho 5
=> 26a - 21b + 2000 chia hết cho 5
Đúng 0
Bình luận (0)
Cho 2a+3b chia hết cho 7.CM a+4b chia hết cho 7
Cho 6a+5b chia hết cho 7.CM a+2b chia hết cho 7
Cho 10a+7b chia het cho 4.Cm 2a+b chia het cho 4
Cho 9a+8c chia het cho 2.Cm a+2b chia het cho 5
a) cho2a + 3b chia hết cho 5 chứng minh ( 3a + 2b ) chia hết cho 5
b) cho 7a + b chia hết cho 11 chứng minh ( 2a + 5b ) chia hết cho 11