cứu cứu xong tui tăng sp cho
cứu cứu xong tui tăng sp cho

Những câu hỏi liên quan
Cứu tui , đọc xong cái bài lú luôn
Bài 1: https://www.liveworksheets.com/gy25424bs
Bài 2: https://www.liveworksheets.com/yn7381no
Cứu tui ik ;-; xong chụp lại màn hình cho tui nha ;-; cám ưn ;^;
Cứu tui mai tui học chx lm xong bài có ngày toid đời
Câu 4 (trang 19 VBT GDCD 9):
Có v thoi
Trong cuộc sống hiện nay, lòng yêu nước thể hiện ở việc cống hiến tài năng, công sức của mình trong việc giữ gìn và xây dựng đất nước, làm rạng rỡ, vinh quang cho quốc gia, dân tộc, có những đóng góp về mặt trí tuệ, những phát minh tiên tiến, những hành động thiết thực vì đất nước. Ngoài ra lòng yêu nước còn thể hiện ở tinh thần đoàn kết vì một mục tiêu chung, không vụ lợi tham ô tham nhũng
Đúng 0
Bình luận (0)
Cứu tui cứu tui

Em tách nhỏ ra để hỏi, không đăng cả đề như thế này, em nhé!
Đúng 2
Bình luận (1)
trời ơi cứu tui cứu tui
Ta có \(\dfrac{a^3}{a^2+b^2}=a-\dfrac{ab^2}{a^2+b^2}\ge a-\dfrac{ab^2}{2ab}=a-\dfrac{b}{2}=\dfrac{2a-b}{2}\)(áp dụng cosi cho \(a^2+b^2\ge2ab\))
\(\dfrac{b^3}{b^2+1}=b-\dfrac{b}{b^2+1}\ge b-\dfrac{b}{2b}=b-\dfrac{1}{2}=\dfrac{2b-1}{2}\)(áp dụng cosi cho\(b^2+1\ge2b\))
\(\dfrac{1}{a^2+1}=1-\dfrac{a^2}{a^2+1}\ge1-\dfrac{a^2}{2a}=1-\dfrac{a}{2}=\dfrac{2-a}{2}\)( áp dụng cosi cho \(a^2+1\ge2a\))
Cộng vế theo vế
\(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+1}+\dfrac{1}{a^2+1}\ge\dfrac{2a-b+2b-1+2-a}{2}\)\(\ge\dfrac{a+b+1}{2}\left(đpcm\right)\)
Dấu "=" xảy ra <=> a=b=1
Đúng 2
Bình luận (0)
Cứu tui trời ưi cứu tui
Cứu tui Cứu tui!
Tìm ước chung lớn nhất và bội chung nhỏ nhất của 36 và 54
Ta có:
\(36=2^2.3^2\)
\(54=2.3^3\)
\(ƯCLN\left(36;54\right)=2.3=6\)
\(BCNN\left(36;54\right)=2^2.3^3=4.27=108\)
Đúng 1
Bình luận (0)
cứu :((tui tick cho
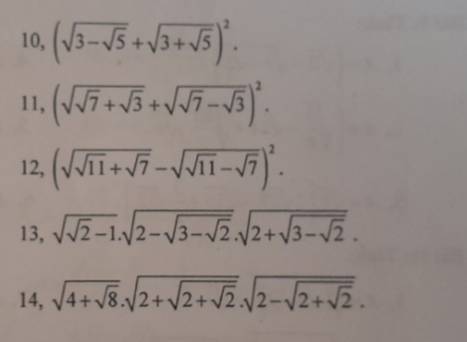
10: \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=\left(\sqrt{3-\sqrt{5}}\right)^2+\left(\sqrt{3+\sqrt{5}}\right)^2+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{9-5}\)
\(=6+2\cdot2=10\)
11: \(\left(\sqrt{\sqrt{7}+\sqrt{3}}+\sqrt{\sqrt{7}-\sqrt{3}}\right)^2\)
\(=\left(\sqrt{\sqrt{7}+\sqrt{3}}\right)^2+\left(\sqrt{\sqrt{7}-\sqrt{3}}\right)^2+2\cdot\sqrt{\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)}\)
\(=\sqrt{7}+\sqrt{3}+\sqrt{7}-\sqrt{3}+2\cdot\sqrt{7-3}\)
\(=2\sqrt{7}+2\cdot2=2\sqrt{7}+4\)
12: \(\left(\sqrt{\sqrt{11}+\sqrt{7}}-\sqrt{\sqrt{11}-\sqrt{7}}\right)^2\)
\(=\left(\sqrt{\sqrt{11}+\sqrt{7}}\right)^2+\left(\sqrt{\sqrt{11}-\sqrt{7}}\right)^2-2\cdot\sqrt{\left(\sqrt{11}-\sqrt{7}\right)\left(\sqrt{11}+\sqrt{7}\right)}\)
\(=\sqrt{11}+\sqrt{7}+\sqrt{11}-\sqrt{7}-2\cdot\sqrt{11-7}\)
\(=2\sqrt{11}-4\)
13:
\(\sqrt{\sqrt{2}-1}\cdot\sqrt{2-\sqrt{3-\sqrt{2}}}\cdot\sqrt{2+\sqrt{3-\sqrt{2}}}\)
\(=\sqrt{\sqrt{2}-1}\cdot\sqrt{4-\left(3-\sqrt{2}\right)}\)
\(=\sqrt{\sqrt{2}-1}\cdot\sqrt{\sqrt{2}+1}\)
\(=\sqrt{2-1}=1\)
14:
\(\sqrt{4+\sqrt{8}}\cdot\sqrt{2+\sqrt{2+\sqrt{2}}}\cdot\sqrt{2-\sqrt{2+\sqrt{2}}}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{\left(2+\sqrt{2+\sqrt{2}}\right)\left(2-\sqrt{2+\sqrt{2}}\right)}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{4-2-\sqrt{2}}\)
\(=\sqrt{\left(4+2\sqrt{2}\right)\left(2-\sqrt{2}\right)}\)
\(=\sqrt{8-4\sqrt{2}+4\sqrt{2}-4}=\sqrt{4}=2\)
Đúng 0
Bình luận (0)
b=3/1x2+3/2x3....+3/50x51 CỨU TUI VỚI NẾU DC MONG CÁC BN GIẢI ĐẦY ĐỦ GIÚP MÌNH NHÉ (AI XONG KB VỚI MÌNH MÌNH CÓ 1 MÓN QUÀ)
\(B=\dfrac{3}{1x2}+\dfrac{3}{2x3}+...+\dfrac{3}{50x51}\)
\(B=3x\left(\dfrac{1}{1x2}+\dfrac{1}{2x3}+...+\dfrac{1}{50x51}\right)\)
\(B=3x\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{50}-\dfrac{1}{51}\right)\)
\(B=3x\left(1-\dfrac{1}{51}\right)=3x\dfrac{50}{51}=\dfrac{150}{51}\)
Đúng 1
Bình luận (0)