Cho tam giác abc cân tại A.Kẻ AH vuông góc với BC tại H.A)Cho AH=4cm;HB=3cm.Tính AB,AC.B)Vẽ HI vuông góc với AB tại I.Trên tia đối của IH lấy điểm K sao cho IH=IK.Chứng minh tam giác AKH cân

Những câu hỏi liên quan
Cho tam giác abc cân tại A.Kẻ AH vuông góc với BC tại H.A)Cho AH=4cm;HB=3cm.Tính AB,AC.B)Vẽ HI vuông góc với AB tại I.Trên tia đối của IH lấy điểm K sao cho IH=IK.Chứng minh tam giác AKH cân
Gấp lắm MN
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh AHB = AHC
b) Cho AH = 4cm; HC = 3cm. Tính độ dài cạnh AC.
c) So sánh góc A và góc B
d) Từ H kẻ HK vuông góc với AB; HM vuông góc với AC (K thuộc AB, M thuộc AC). Chứng minh KB = MC
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: AC=5cm
d: Xét ΔKBH vuông tại K và ΔMCH vuông tại M có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔKBH=ΔMCH
Suy ra: KB=MC
Đúng 0
Bình luận (0)
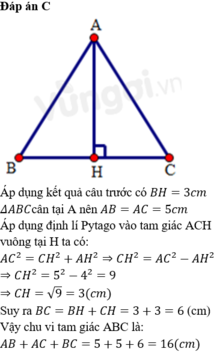
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho AH=4cm,AB=5cm
Chu vi tam giác ABC
A. 18 (cm)
B. 15 (cm)
C. 16 (cm)
D. 20 (cm)
cho tam giác ABC cân tại A.kẻ AH vuông góc BC tại H.kẻ HM vuông góc AB và HN vuông góc AC chứng minh
a)tam giác BMH =tam giác CNH
b)tam giác AMN cân
c)AH vuông góc MN
giúp mik vs please 🥺🥺🥺
a: Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
b: Ta có: ΔBMH=ΔCNH
nên BM=CN
=>AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
mà AH⊥BC
nên AH⊥MN
Đúng 1
Bình luận (1)
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) C/m: tam giác AHB= tam giác AHC
b) Kẻ HM vuông góc với AB tại M. Kẻ HN vuông góc với C tại N. C/m: tam giác AMN cân
c) C/m: AH vuông góc với MN
Giải nhanh giúp mik với ạ. Mai mik phải thi rồi🥺🥺
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAHM vuông tại M và ΔAHN vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAHM=ΔAHN
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Ta có: AM=AN
HM=HN
Do đó: AH là đường trung trực của MN
hay AH⊥MN
Đúng 6
Bình luận (1)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
cạnh AH chung
AB=AC(vì tam giác ABC cân tại A)
=> ΔAHB=ΔAHC(c.h-c.g.v)
Xét ΔAHM vuông tại M và ΔAHN vuông tại N có
\(\widehat{HAM}=\widehat{HAN}\)
cạnh AH chung
==> ΔAHM=ΔAHN(c.h-g.n)
==> AM=AN
=> ΔAMN cân tại A ( dấu hiệu)
c)Ta có:HM=HN ; AM=AN
===>AH là đường trung trực của MN
=>\(\text{AH⊥MN}\)
Đúng 3
Bình luận (2)
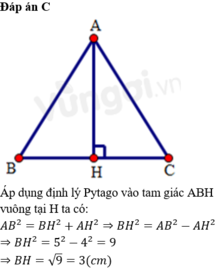
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho AH=4cm,AB=5cm
Tính BH
A. 2 (cm)
B. 5 (cm)
C. 3 (cm)
D. 4 (cm)
Cho tam giác ABC cân có AB=AC=5cm, BC= 8cm . Kẻ AH vuông góc với BC tại H.
a) chứng minh: AH là tia phân giác của A.
b) Tính độ dài AH.
c) Kẻ HD vuông góc với AB ( D thuộc AB), Kẻ HE vuông góc với AC ( E thuộc AC) chứng minh tam giác HDE là tam giác cân.
có vẽ hình ạ
a) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC).
=> AH là đường phân giác góc A (Tính chất tam giác cân).
b) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC).
=> AH là đường trung tuyến (Tính chất tam giác cân).
=> H là trung điểm của BC.
=> BH = HC = \(\dfrac{1}{2}\) BC = \(\dfrac{1}{2}\).8 = 4 (cm).
Xét tam giác AHB vuông tại A:
Ta có: \(AB^2=AH^2+BH^2H^2\) (Định lý Pytago).
=> \(5^2=AH^2+4^2.\) => \(AH^2=5^2-4^2=9.\)
=> AH = 3 (cm).
c) Xét tam giác AHD vuông tại D và tam giác AHE vuông tại A:
AH chung.
Góc DAH = Góc EAH (AH là đường phân giác góc A).
=> Tam giác AHD = Tam giác AHE (ch - gn).
=> HD = HE (2 cạnh tương ứng).
=> Tam giác DHE cân tại H.
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A.Kẻ AH vuông góc BC tại H .Trên tia đối của HA lấy điểm M sao cho AH=HM. a) Chứng minh tam giác ABH=tam giác MBH. b) Trên tia đối của tia CA lấy điểm N sao cho CA=CN.Chứng minh tam giác CMN cân. c) Chứng minh AM vuông góc với MN.
a,Ta có:
\(AH\perp BC\) nên \(\widehat{AHB}\) +90 độ.
Vì M là tia đối của HA nên \(\widehat{MHB}\)= 90 độ.
Xét \(\Delta ABH\) và \(\Delta MBH\)có
AH = MH (gt)
\(\widehat{AHB}\) = \(\widehat{MHB}\) (= 90 độ )
BH : cạnh chung
\(\Rightarrow\Delta ABH=\Delta MBH\)( c.g.c )
b,Xét \(\Delta AHCv\text{à}\Delta MHC\)Ta có:
AH = HM (gt)
\(\widehat{AHC}\)= \(\widehat{MHC}\)(= 90 độ)
HC : cạnh chung
\(\Rightarrow\Delta AHC=\Delta MHC\)( c.g.c)
\(\Rightarrow\)AC=CM ( t/ứ)
Mà AC = CN (gt) và CM = AC (cmt)
nên CM = CN
\(\Rightarrow\Delta CMN\)cân
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.a)Chứng minh: ΔAHB ΔAHC.b)Chứng minh: HB HC và góc BAH góc CAHc)Kẻ HK vuông góc với AB tại K và HI vuông góc với AC tại I. Chứng minh: ΔHKB ΔHIC.Bài 2: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D.Kẻ DK⊥AB tại K.a)Chứng minh ΔABDΔKBD.b)Tia KD cắt tia BA tại M. Chứng minh AMKC và ΔBMC cân.c)Chứng minh AK // MC.Chứng minh BD⊥MC.
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.
a)Chứng minh: ΔAHB = ΔAHC.
b)Chứng minh: HB = HC và góc BAH = góc CAH
c)Kẻ HK vuông góc với AB tại K và HI vuông góc với AC tại I.
Chứng minh: ΔHKB = ΔHIC.
Bài 2: Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D.
Kẻ DK⊥AB tại K.
a)Chứng minh ΔABD=ΔKBD.
b)Tia KD cắt tia BA tại M. Chứng minh AM=KC và ΔBMC cân.
c)Chứng minh AK // MC.
Chứng minh BD⊥MC.
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔABH=ΔACH
nên HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔHKB vuông tại K và ΔHIC vuông tại I có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHKB=ΔHIC
Đúng 0
Bình luận (0)