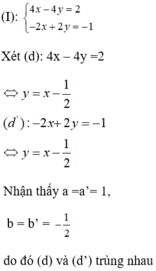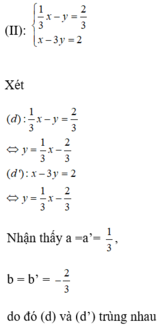Đoán nhận số nghiệm của hệ phương trình sau và giải thích vì sao x-2y=3 -2x+3y=6
Những câu hỏi liên quan
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a
)
4
x
−
4
y
2
−
2
x...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a ) 4 x − 4 y = 2 − 2 x + 2 y = − 1 b ) 1 3 x − y = 2 3 x − 3 y = 2
a)
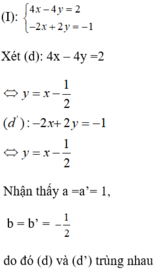
Vậy hệ phương trình có vô số nghiệm.
b)
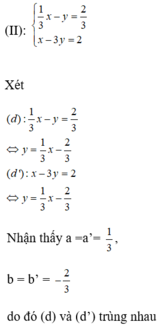
Vậy hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I):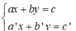 
Gọi (d): ax + b = c và (d’): a’x + b’ = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’
Đúng 0
Bình luận (0)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a
)
x
+
y
2
3
x
+
3
y...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
a ) x + y = 2 3 x + 3 y = 2 b ) 3 x − 2 y = 1 − 6 x + 4 y = 0
a) (I):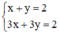 
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x +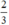 
có a’ = -1 ; b’ =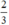 
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.
b) (II):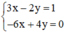 
Xét: (d): 3x – 2y = 1 hay (d):
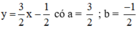
(d’): -6x + 4y = 0 hay (d’):
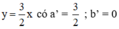
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.
Kiến thức áp dụng
+ Xét hệ (I):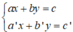 
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
Đúng 0
Bình luận (0)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
4
x
-
4
y
2
-
2
x
+
2
y
-...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
4 x - 4 y = 2 - 2 x + 2 y = - 1
18 tháng 1 2023 lúc 18:19
Đoán nhận hệ số nghiệm của mỗi hệ phương trình sau và giải thích vì sao:a) left{{}begin{matrix}2x+y33x-y1end{matrix}right.b) left{{}begin{matrix}3x+2y02x-3y0end{matrix}right.c) left{{}begin{matrix}3x+0y62x+y1end{matrix}right. d) left{{}begin{matrix}x-y40x-y2end{matrix}right.e) left{{}begin{matrix}x+2y32x+4y1end{matrix}right.f) left{{}begin{matrix}x+y1dfrac{x}{2}+dfrac{y}{2}dfrac{1}{2}end{matrix}right.Mẫu câu a : Ta có: dfrac{a}{a}nedfrac{b}{b}Leftrightarrowdfrac{2}{3}nedfrac{1}{-1}, do đó hệ phư...
Đọc tiếp
Đoán nhận hệ số nghiệm của mỗi hệ phương trình sau và giải thích vì sao:
a) \(\left\{{}\begin{matrix}2x+y=3\\3x-y=1\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}3x+2y=0\\2x-3y=0\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}3x+0y=6\\2x+y=1\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}x-y=4\\0x-y=2\end{matrix}\right.\)
e) \(\left\{{}\begin{matrix}x+2y=3\\2x+4y=1\end{matrix}\right.\)
f) \(\left\{{}\begin{matrix}x+y=1\\\dfrac{x}{2}+\dfrac{y}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Mẫu câu a : Ta có: \(\dfrac{a}{a'}\ne\dfrac{b}{b'}\Leftrightarrow\dfrac{2}{3}\ne\dfrac{1}{-1}\), do đó hệ phương trình đã cho có 1 nghiệm duy nhất
giúp mk vs mn ơi! mk đang cần gấp
b: \(\dfrac{3}{2}< >\dfrac{2}{-3}\)
nên hệ có 1 nghiệm duy nhất
c: 3/2<>0/1
nên hệ có 1 nghiệmduy nhất
d: 0/1<>-1/-1
nên hệ có 1 nghiệm duy nhất
e: 1/2=2/4<>3/1
nên hệ ko có nghiệm
f: 1:1/2=1:1/2=1:1/2
nên hệ có vô số nghiệm
Đúng 1
Bình luận (0)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao: x + y = 2 3 x + 3 y = 2
(I):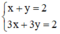 
Xét (d): x + y = 2 hay (d): y = -x + 2 có a = -1; b = 2.
(d’) 3x + 3y = 2 hay (d’): y = -x +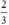 
có a’ = -1 ; b’ =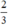 
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (I) vô nghiệm.
Đúng 0
Bình luận (0)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
1
3
x
-
y
2
3
x
-
3
y...
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
1 3 x - y = 2 3 x - 3 y = 2
Hãy biểu diễn y qua x ở mỗi phương trình (nếu có thể) rồi đoán nhận số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao (không vẽ đồ thị).
4
x
-
9
y
3
-
5
x...
Đọc tiếp
Hãy biểu diễn y qua x ở mỗi phương trình (nếu có thể) rồi đoán nhận số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao (không vẽ đồ thị).
4 x - 9 y = 3 - 5 x - 3 y = 1
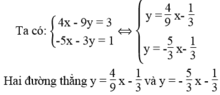
cắt nhau vì chúng có hệ số góc khác nhau.
Vậy hệ phương trình có một nghiệm duy nhất.
Đúng 0
Bình luận (0)
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
3
x
-
2
y
1
-
6
x
+
4
y
0
Đọc tiếp
Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:
3 x - 2 y = 1 - 6 x + 4 y = 0
(II):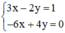 
Xét: (d): 3x – 2y = 1 hay (d):
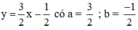
(d’): -6x + 4y = 0 hay (d’):
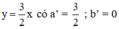
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.
Đúng 0
Bình luận (0)
Hãy biểu diễn y qua x ở mỗi phương trình (nếu có thể) rồi đoán nhận số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao (không vẽ đồ thị).
3
x
-
y
1
6
x
-
2...
Đọc tiếp
Hãy biểu diễn y qua x ở mỗi phương trình (nếu có thể) rồi đoán nhận số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao (không vẽ đồ thị).
3 x - y = 1 6 x - 2 y = 5
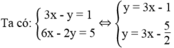
Vì hai đường thẳng có hệ số góc đều bằng 3 nhưng tung độ gốc khác nhau (-1 ≠ - 5/2 ) nên chúng song song với nhau.
Vậy hệ phương trình vô nghiệm.
Đúng 0
Bình luận (0)