Xét dấu biểu thức y=(x-1)^2

Những câu hỏi liên quan
Xét dấu biểu thức sau: f(x,y)= 3x^2 + y^2 - 2x - xy + y +3
\(f\left(x;y\right)=3x^2+y^2-2x-xy+y+3\)
\(=\left(x^2-xy+\dfrac{y^2}{4}\right)+\dfrac{1}{2}\left(4x^2-4x+1\right)+\dfrac{1}{3}\left(\dfrac{9}{4}y^2+3y+1\right)+\dfrac{13}{6}\)
\(=\left(x-\dfrac{y}{2}\right)^2+\dfrac{1}{2}\left(2x-1\right)^2+\dfrac{1}{3}\left(\dfrac{3y}{4}+1\right)^2+\dfrac{13}{6}>0;\forall x;y\)
Đúng 0
Bình luận (0)
Xét dấu của biểu thức sau :
f(x) = (1+x)(x-2)^2(4-x)
Xem chi tiết
Xét f(x) = (1+x)(x-2)2(4-x)
f(x) = 0 \(\Leftrightarrow\) x = -1 hoặc x = 2 hoặc x = 4
ta có bảng
x \(-\infty\) -1 2 4 \(+\infty\)
1+x - 0 + | + | +
(x-2)2 + | + 0 + | +
4-x + | + | + 0 -
f(x) - 0 + 0 + 0 -
Chúc bn học tốt
Đúng 1
Bình luận (0)
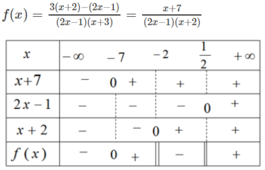
Xét dấu biểu thức sau: f ( x ) = 3 2 x - 1 - 1 x + 2
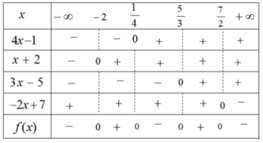
Xét dấu biểu thức sau: f(x) = (4x - 1)(x + 2)(3x - 5)(-2x + 7)
f(x)=(3x+1)/(x+1)-(4)/(x^(2)-2x+1)
Xét dấu biểu thức ạ ai giúp mình với
Xét dấu biểu thức f(x) = (2x – 1)(-x + 3)

Các nghiệm này chia khoảng thành ba khoảng, trong mỗi khoảng các nhị thức đã cho có dấu hoàn toàn xác định.

Từ bảng xét dấu ta thấy:
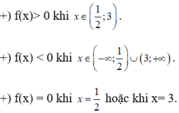
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 92: Giải bất phương trình x3 – 4x < 0.
Lời giải
x3 – 4x < 0 ⇔ x(x2 - 4) < 0 ⇔ x(x - 2)(x + 2) < 0
Ta có bảng xét dấu

Từ bảng xét dấu ta có tập nghiệm của bất phương trình là:
S = (-∞;2) ∪ (0;2)
Đúng 0
Bình luận (0)
Xét dấu biểu thức: f(x) = (2x - 1)(x + 3)
Nhị thức 2x – 1 có nghiệm là 1/2 ; nhị thức x + 3 có nghiệm là –3.
Ta có bảng xét dấu
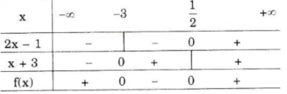
Kết luận :
+ f(x) > 0 khi x < –3 hoặc x > 1/2
+ f(x) < 0 khi –3 < x < 1/2
+ f(x) = 0 khi x = –3 hoặc x = 1/2.
Đúng 0
Bình luận (0)
Xét dấu biểu thức sau đây:\(f\left(x\right)=\) \(\dfrac{2x+3}{x+1}+\dfrac{x+6}{-3x-2}\)
Bài 3: Xét dấu các biểu thức sau 1/ f(x) = (2x - 1)(x ^ 3 - 1)
. 2 / (f(x)) = (- 2x ^ 2 + 7x + 7)/(x ^ 2 - 3x - 10) - 1