Cho tam giác ABC vuông ở A. Vẽ trung tuyến AM ; M thuộc cạnh BC. Trên tia AN lấy AM' sao cho AM' = 2AM
a) CMR : Tam giác ACM' vuông tại C
b) CMR : Tam giác ABC = Tam giác ACM
c) CMR : AM = 1/2 BC
cho tam giác ABC , kẻ trung tuyến AM. Ở phía ngoài tam giác ABC vẽ các tam giác vuông cân tại A là ABE và ACG .Chứng minh :
a) AB//CD(D thuộc tia đối tia MA sao cho MD=MA)
b) AM VUÔNG GÓC EG
Cho tam giác ABC cân tại A trung tuyến AM D thuộc tia đối của AC sao cho AD=AC vẽ AE vuông góc BD a) c/m AM vuông góc BC b) c/m tam giác BDC vuông ở B c) c/m EB=ED d) EM//CD
a: ΔABC cân tại A có AM là trung tuyến
nên AM vuông góc BC
b: Xét ΔDBC có
BA là trung tuyến
BA=CD/2
=>ΔDBC vuông tại B
c: ΔABD cân tại A có AE là đường cao
nên E là trung điểm của BD
d: Xét ΔDBC có BE/BD=BM/BC
nên EM//DC
Cho tam giác ABC, trung tuyến AM. Vẽ ra phía ngoài tam giác các tam giác vuông cân ở A là tam giác ABD và tam giác ACE.
a, F là tia đối của tia AM: MF = AM. Chứng minh: góc ABF = góc DAE.
b, DE = 2AM.
cho tam giác abc vuông tại a, vẽ trung tuyến am, truung trực cd,
Cho tam giác ABC vuông tại A, B ^ = 35 0 và AB = 6cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABC
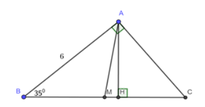
Giải tam giác ABC.
A. AC = 8,57cm; BC = 10,46cm; C ^ = 55 0 .
B. AC = 4,9cm; BC = 7,75cm; C ^ = 55 0 .
C. AC = 4,2cm; BC = 7,32cm; C ^ = 55 0 .
D. AC = 3,44cm; BC = 6,92cm; C ^ = 55 0 .
Xét ∆ ABC vuông tại A ta có:
Vì ∆ ABC vuông tại A ta có:
![]()
Đáp án cần chọn là: C
cho tam giác abc vuông tại a có ab =5 ac =12 . vẽ trung tuyến am của tam giác abc . trên tia đối của tia am lấy điểm k sao cho mk =ma
a, vẽ hình
b,chứng minh tam giác mkc =tam giác mab .từ đó suy ra kc vuông góc vs ac
c, tính độ dài am
b,- Ta có : AM là đường trung tuyến của tam giác vuông ABC .
=> AM = BM = CM = KM .
Xét \(\Delta MKC\) và \(\Delta MAB\) có :
\(\left\{{}\begin{matrix}BM=MC\\AM=MK\\\widehat{BMA}=\widehat{KMC}\end{matrix}\right.\)
=> \(\Delta MKC\) = \(\Delta MAB\) ( c - g - c )
- Xét tứ giác ABKC có :
AM = BM = CM = KM và tam giác ABC vuông tại A .
=> Tứ giác ABKC là hình chữ nhật.
=> KC vuông góc với AC .
c, - Áp dụng định lý pitago vào tam giác ABC vuông tại A :
\(BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\)
Ta có : \(AM=\dfrac{1}{2}BC=\dfrac{13}{2}\)
bài 20 cho tam giác abc vuông ở a (ab < ac) , đường trung tuyến am, đường cao ah. qua h vẽ đường thẳng vuông góc với ac, cắt am tại n. chứng minh tứ giác abhn là hình thang cân.
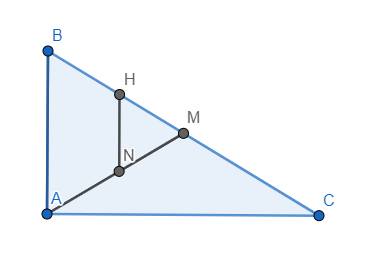
Ta có \(HN\perp AC\) và \(AB\perp AC\) nên AB//HN. Do đó tứ giác ABHN là hình thang (1)
Mặt khác, tam giác ABC vuông tại A có trung tuyến AM nên \(AM=\dfrac{1}{2}BC=BM\), suy ra tam giác MAB cân tại M hay \(\widehat{ABH}=\widehat{NAB}\) (2)
Từ (1) và (2), ta suy ra tứ giác ABHN là hình thang cân. (đpcm)
Cho tam giác ABC cân ở A ( A<90 ). Có AM là trung tuyến Cm
a Tam giác ABM = Tam Giac ACM, AM là phân giác góc A
bTừ M vẽ ME vuông Với AB , MF vuông với AC . CM tam Giacs MAE = tam giác MAF
Tam giác AEF cân
c TRên tia đối của tia MA lấy H sao cho Ma=MH Gọi N là trung điiểm của CH , I là giao điiểm của CB và AN . cm MI=1/6 BC
a: Xét ΔABM và ΔACM co
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: Xét ΔAME vuông tại E và ΔAMF vuông tại F có
AM chung
góc MAE=góc MAF
=>ΔAME=ΔAMF
=>AE=AF
=>ΔAEF cân tại A
Cho tam giác ABC, vẽ trung tuyến AM, BN, CP sao cho BN vuông góc với AM. Trên tia đối của tia MN lấy điểm Q sao cho MQ = MN .
a ) So sánh các cạnh của tam giác CPQ và các đường trung tuyến của tam giác ABC
b) C/m tam giác PQC là tam giác vuông
Xét tam giác QMC và tam giác NMB có:
BM=CN(giả thiết)
NM=NQ(GT)
BMN=QMC(đối đỉnh)
\(\Rightarrow\)2 tam giác = nhau
\(\Rightarrow\)QC=BN(2 cạnh tương ứng)
+)Ta có:N trung điểm AC
M trung điểm BC
Nên áp dụng bài toàn phụ về đường trung bình(ko biết thì nhớ search)
\(\Rightarrow\)MN//AB,MN=AB/2
\(\Rightarrow\)MQ//AB,MQ=AB/2(MN=MQ)
\(\Rightarrow\)MQ//AB,MQ=AP(AP=AB/2)
Ta có :MQ//AP<MQ=AP
Nên áp dụng tính chất đoạn chắn (tự search dùm nếu ko bít)
\(\Rightarrow\)AM=PQ.
(Kết luận thì tự đi mà viết mỏi tay VCL!!!)
Để phòng tránh copy ,vui lòng k cho vũ văn đạt đầu tiên
Câu b) tui đang nghĩ nha ! Chắc phải vài tiếng