Tìm 3 số tự nhiên lập thành cấp số cộng có tổng 366 . Biết số thứ 3 bằng 3 lần số thứ nhất

Những câu hỏi liên quan
Ba số tự nhiên lập thành một cấp số cộng có tổng bằng 180. Tìm ba số biết số thứ ba gấp 3 lần số thứ nhất
Vì ba số tự nhiên lập thành một cấp số và số thứ ba gấp 3 lần số thứ nhất
=>số thứ 2 gấp 2 lần số thứ nhất
Số thứ nhất là:
180:(1+2+3)*1=30
Số thứ hai là:
180:(1+2+3)*2=60
Số thứ ba là:
180:(1+2+3)*3=90
Đúng 0
Bình luận (0)
30 + 60 = 90. Vậy ba số có số là : 30, 60, 90
Đúng 0
Bình luận (0)
Tìm ba số, biết theo thứ tự đó chúng lập thành cấp số cộng và có tổng bằng 21, và nếu lần lượt cộng thêm các số 2;3;9 vào ba số đó thì được ba số lập thành một cấp số nhân.
Gọi 3 số cần tìm lần lượt là: \({u_{n - 1}},\;{u_n},\;{u_{n + 1}}\)
Theo tính chất của cấp số cộng ta có: \({u_{n - 1}} + {u_{n + 1}} = 2{u_n}\)
Mà đề bài: \({u_{n - 1}} + {u_n} + {u_{n + 1}} = 21\) suy ra \(3{u_n} = 21\;\)
\(\begin{array}{l} \Leftrightarrow {u_n} = 7\\ \Leftrightarrow \left\{ \begin{array}{l}{u_{n - 1}} = {u_n} - d = 7 - d\\{u_{n + 1}} = {u_n} + d = 7 + d\end{array} \right.\end{array}\)
Lần lượt cộng thêm các số 2, 3, 9 vào 3 số ta được: \({u_{n - 1}} + 2,\;{u_n} + 3,\;{u_{n + 1}} + 9\) hay \(9 - d,\;10,\;16 + d\)
Theo tính chất của cấp số nhân ta có:
\(\begin{array}{l}\left( {9 - d} \right)\left( {16 + d} \right) = {10^2}\\ \Leftrightarrow {d^2} + 7d - 44 = 0\\ \Leftrightarrow \left[ \begin{array}{l}d = - 11\\d = 4\end{array} \right.\end{array}\)
Vậy 3 số cần tìm là: 18; 7; -4 hoặc 3; 7; 11.
Đúng 0
Bình luận (0)
tìm 3 stn lập thành cấp số cộng có tổng = 1080 và số thứ 3 = 5 lần số thứ 1
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính
F
x
2
+
y
2
+
z
2
A. F 389 hoặc F 179 B. F 441 hoặc F...
Đọc tiếp
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính F = x 2 + y 2 + z 2
A. F = 389 hoặc F = 179
B. F = 441 hoặc F = 357
C. F = 395 hoặc F = 179
D. F = 389 hoặc F = 395
Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
⇔ x + z - 2 y
Và số x, y, z lập thành một cấp số nhân ⇔ x z = y 2
Cách giải
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
x + z = 2 y x + y + z = 21
⇔ x + z = 14 y = 7
⇔ x = 14 - z y = 7 ( 1 )
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng)
thì được ba số lập thành một cấp số nhân nên ta có
( x + 2 ) ( z + 9 ) = ( y + 3 ) 2 ( 2 )
Thay (1) vào (2) ta có:
( 14 - z + 2 ) ( z + 9 ) = ( 7 + 3 ) 2
⇔ z 2 - 7 z - 44 = 0
⇔ z = 11 z = - 4
z = 11 ⇒ z = 14 - 11 = 3
⇒ F = x 2 + y 2 + z 2 = 179
z = - 4 ⇒ x = 14 - ( - 4 ) = 18
⇒ F = x 2 + y 2 + z 2 = 389
Đúng 0
Bình luận (0)
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính
F
x
2
+
y
2
+
z
2
.
A. F 389 hoặc F 179 B. F 441 hoặc F 357 C. F 395 hoặc F 179 D. F 389 hoặc F 395
Đọc tiếp
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính F = x 2 + y 2 + z 2 .
A. F = 389 hoặc F = 179
B. F = 441 hoặc F = 357
C. F = 395 hoặc F = 179
D. F = 389 hoặc F = 395
Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
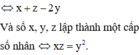
Cách giải:
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
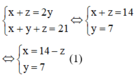
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân nên ta có:
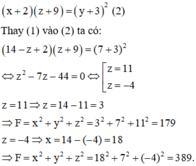
Đúng 0
Bình luận (0)
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2 ; 3 ; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính
F
x
2
+
y
2
+
z
2
.
A. F389 Hoặc F395 B.F395 Hoặc F179 C.F389 Hoặc F179 D.F441 Hoặc F357
Đọc tiếp
Ba số x, y, z lập thành một cấp số cộng và có tổng bằng 21. Nếu lần lượt thêm các số 2 ; 3 ; 9 vào ba số đó (theo thứ tự của cấp số cộng) thì được ba số lập thành một cấp số nhân. Tính F = x 2 + y 2 + z 2 .
A. F=389 Hoặc F=395
B.F=395 Hoặc F=179
C.F=389 Hoặc F=179
D.F=441 Hoặc F=357
Chọn C
*Theo tính chất của cấp số cộng , ta có x+ z = 2y.
Kết hợp với giả thiết, x+ y + z = 21, ta suy ra 3y = 21 nên y = 7.
* Gọi d là công sai của cấp số cộng thì x = y − d = 7 − d và z = y + d = 7 + d .
Sau khi thêm các số 2 ; 3 ; 9 vào ba số x ; y ; z ta được ba số là x+ 2 ; y + 3 ; z + 9 hay
9- d ; 10 ; 16+ d.
* Theo tính chất của cấp số nhân, ta có
9 − d 16 + d = 10 2 ⇔ d 2 + 7 d − 44 = 0
Giải phương trình ta được d= -11 hoặc d= 4.
Với d = -11 ; cấp số cộng 18 ; 7 ; - 4. Lúc này F = 389.
Với d= 4, cấp số cộng 3 ; 7 ; 11. Lúc này F = 179.
Đúng 0
Bình luận (0)
Các số a,b,c (theo thứ tự đó) lập thành một cấp số nhân có tổng bằng 26. Tìm các số đó biết rằng: nếu một cấp số cộng có a là số hạng thứ nhất, b là số hạng thứ ba thì c là số hạng thứ chín
Gọi công bội của cấp số nhân là q => b=a.q; c=a.q^2
Gọi công sai của cấp số cộng là d => b=a+2d; c=a+8d
Ta có: a.q=a+2d => \(q=\dfrac{a+2d}{a}=1+2\dfrac{d}{a}\)
\(a.q^2=a+8d\Rightarrow q^2=\dfrac{a+8d}{a}=1+8\dfrac{d}{a}\)
Suy ra \(\left(1+2\dfrac{d}{a}\right)^2=1+8\dfrac{d}{a}\Rightarrow\dfrac{d}{a}=1\left(d\ne0\right)\)
=> b=a+2a=3a; c=a+8a=9a
Theo bài ra a+b+c=26 => a+3a+9a=13a=26 => a=2; b=6; c=18
Vậy ba số cần tìm là a=2; b=6; c=18
Đúng 1
Bình luận (0)
Cho 3 số tạo thành một cấp số cộng có tổng 21. Nếu thêm 2, 3, 9 lần lượt vào số thứ nhất, số thứ hai, số thứ ba tạo thành một cấp số nhân. Tìm 3 số đó.
A. 3, 7, 11
B. 3; 8; 10
C. 18, 7, -4
D. Đáp án khác
Chọn D.
Gọi u1; u2; u3 tạo thành cấp số cộng.
Theo đề bài: u1 + 2; u2 + 3; u3 + 9 là ba số liên tiếp tạo thành cấp số nhân.
Theo đề bài: 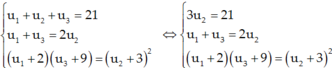
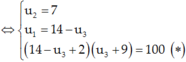
Giải (*): (16 – u3)(u3 + 9) = 100 ⇔ -u32 + 7u3 + 44 = 0 ⇔ u3 =11 ∨ u3 = - 4
Với u3 = 11 ⇒ u1 = 3.
Với u3 = -4 ⇒ u1 = 18.
Đúng 0
Bình luận (0)
Bài 1 : Tìm hai số tự nhiên biết rằng tổng của chúng là 100 và số thứ nhất gấp 4 lần số thứ haiBài 2 : Tìm hai số tự nhiên biết rằng hiệu của chúng là 10 và 2 lần số thứ nhất bằng 3 lần số thứ haiBài 3 : Tìm số tự nhiên có hai chữ số biết rằng chữ số hàng chục bé hơn chữ số hàng đơn vị là 3. Nếu đổi chỗ hai chữ số của nó thì được số mới biết rằng tổng của số mới và ban đầu là 77
Đọc tiếp
Bài 1 : Tìm hai số tự nhiên biết rằng tổng của chúng là 100 và số thứ nhất gấp 4 lần số thứ hai
Bài 2 : Tìm hai số tự nhiên biết rằng hiệu của chúng là 10 và 2 lần số thứ nhất bằng 3 lần số thứ hai
Bài 3 : Tìm số tự nhiên có hai chữ số biết rằng chữ số hàng chục bé hơn chữ số hàng đơn vị là 3. Nếu đổi chỗ hai chữ số của nó thì được số mới biết rằng tổng của số mới và ban đầu là 77
Bài 1:
Gọi hai số tự nhiên cần tìm là a,b
Số thứ nhất gấp 4 lần số thứ hai nên a=4b(1)
Tổng của hai số là 100 nên a+b=100(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a=4b\\a+b=100\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4b+b=100\\a=4b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=100\\a=4b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=\dfrac{100}{5}=20\\a=4\cdot20=80\end{matrix}\right.\)
Bài 2:
Gọi hai số cần tìm là a,b
Hiệu của hai số là 10 nên a-b=10(4)
Hai lần số thứ nhất bằng ba lần số thứ hai nên 2a=3b(3)
Từ (3) và (4) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=10\\2a=3b\end{matrix}\right.\Leftrightarrow\)\(\left\{{}\begin{matrix}a-b=10\\2a-3b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a-2b=20\\2a-3b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a-2b-2a+3b=20\\2a=3b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\2a=3\cdot20=60\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=30\\b=20\end{matrix}\right.\)
Bài 3:
Gọi số tự nhiên cần tìm có dạng là \(\overline{ab}\left(a\ne0\right)\)
Chữ số hàng chục bé hơn chữ số hàng đơn vị là 3 nên b-a=3(5)
Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới lập ra và số ban đầu là 77 nên ta có:
\(\overline{ab}+\overline{ba}=77\)
=>\(10a+b+10b+a=77\)
=>11a+11b=77
=>a+b=7(6)
Từ (5) và (6) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=5\\a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-a+b+a+b=5+7\\a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2b=12\\a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6\\a=7-6=1\end{matrix}\right.\)
Vậy: Số tự nhiên cần tìm là 16
Đúng 1
Bình luận (0)
















