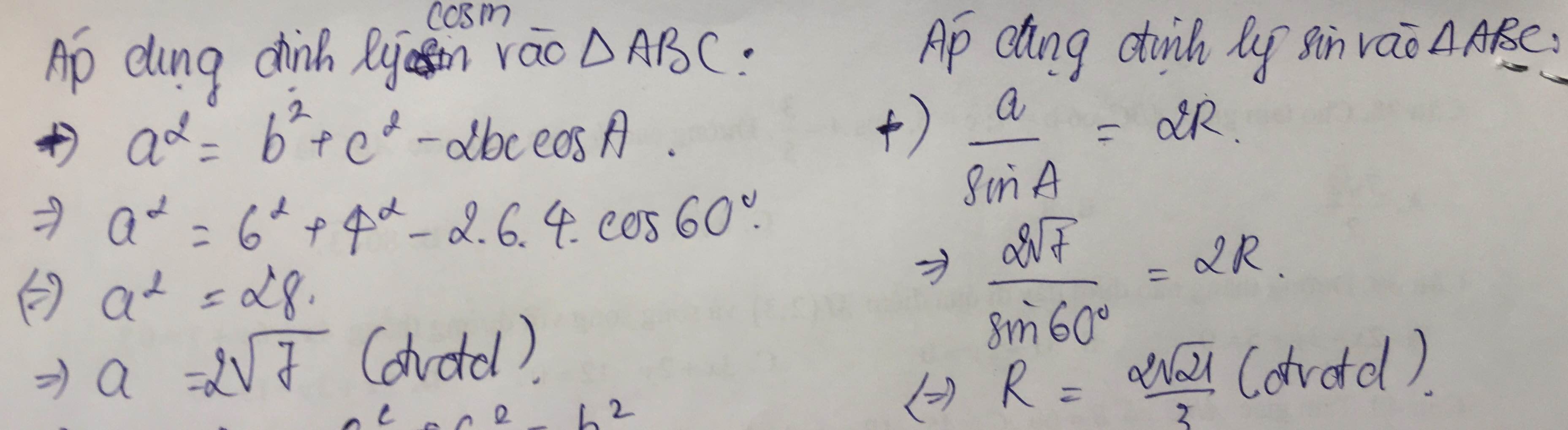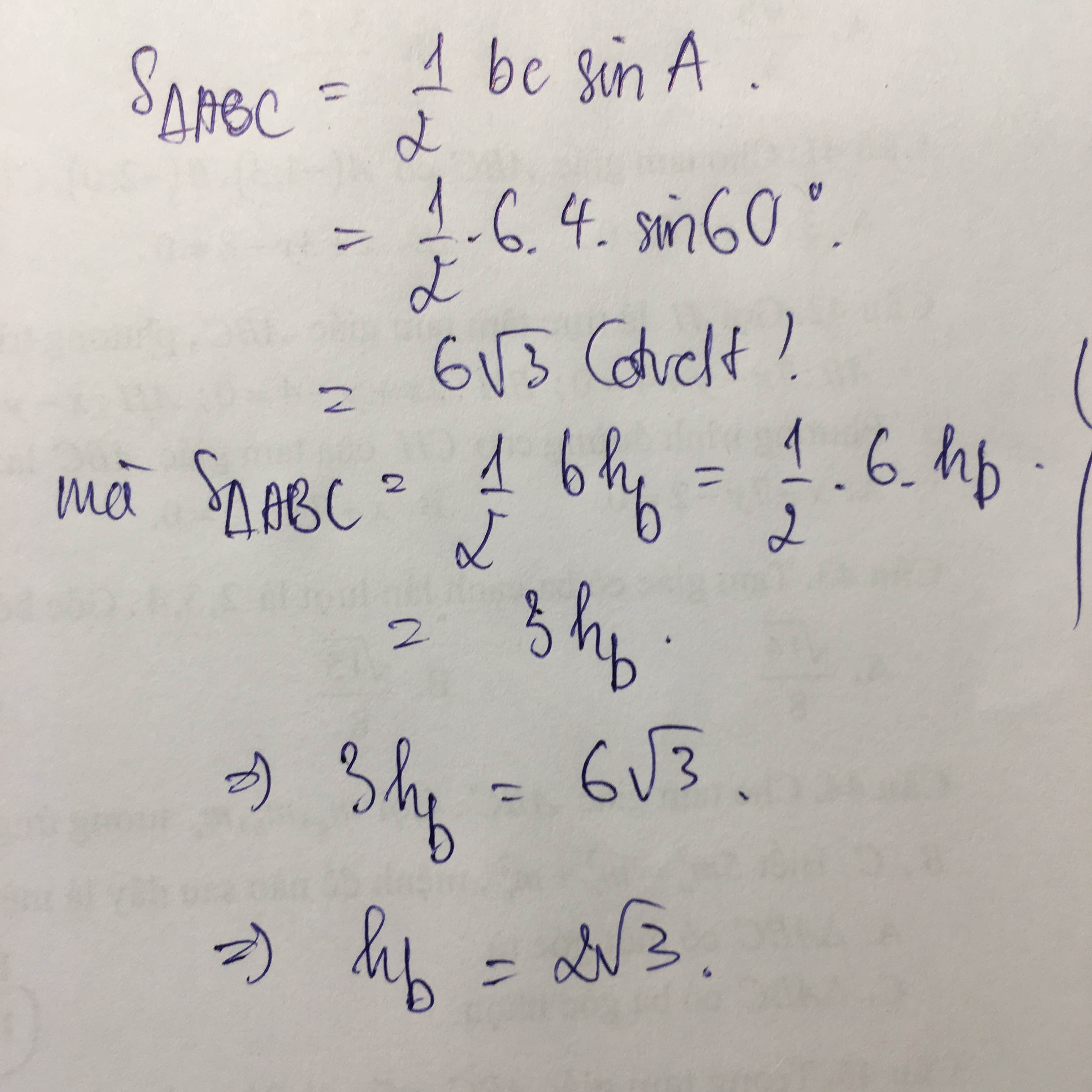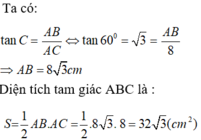Những câu hỏi liên quan
Cho tam giác ABC có AB = AC. Tam giác ABC không là tam giác đều nếu thỏa mãn điều kiện:
A. B ^ = 60 ° .
B. AB = BC.
C. AB < BC.
D. A ^ = 60 ° .
Cho tam giác ABC có AC =16,A=60°,C=50° .Tính diện tích tam giác ABC.
Cho tam giác ABC có góc A = 60 độ trên BC lấy M sao cho BM = 2MC và góc AMB =60 độ. tính các góc tam giác ABC
Cho tam giác ABC có góc A=60° C=45° R=5 tính diện tích tam giác ABC
\(\widehat{B}=180^o-60^o-45^o=75^o\)
Theo định lý sin ta có:
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=\dfrac{AB\cdot sinB}{sinC}=\dfrac{5\cdot sin75^o}{sin45^o}=\dfrac{5+5\sqrt{3}}{2}\)
Mà: \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot5\cdot\dfrac{5+5\sqrt{3}}{2}\cdot sin60^o=\dfrac{75+25\sqrt{3}}{8}\left(dvdt\right)\)
Đúng 1
Bình luận (2)
cho tam giác ABC có AC =16, góc A=60, góc C=50. tính diện tích tam giác ABC
29 tháng 3 2022 lúc 8:19
Cho tam giác ABC có b = 6cm, c = 4cm, góc A = 60 độ. Tính cạnh a, bán kính đường tròn ngoại tiếp tam giác ABC, đường cao Bh của tam giác ABC
Cho tam giác ABC vuông tại A có AC 8cm và góc C 60
°
. Tính diện tích tam giác ABC . A. 32
c
m
2
B. 16
3
c
m
2
C. 16
c
m
2
D. 32
3
c
m
2
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 8cm và góc C = 60 ° . Tính diện tích tam giác ABC .
A. 32 c m 2
B. 16 3 c m 2
C. 16 c m 2
D. 32 3 c m 2
Cho tam giác ABC cân tại A có góc B bằng \({60^o}\). Chứng minh rằng tam giác ABC đều.
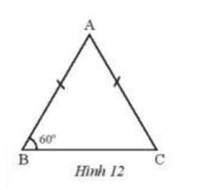
Ta có: tam giác ABC cân tại A
Nên \(\widehat B = \widehat C = {60^o}\)( 2 góc đáy của tam giác cân )
Theo định lí về tổng 3 góc trong tam giác ta có : \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat A = {180^o} - {60^o} - {60^o} = {60^o}\)
Vì \(\widehat A = \widehat B = \widehat C = {60^o}\)\( \Rightarrow \) tam giác ABC là tam giác đều
Đúng 0
Bình luận (0)
17 tháng 4 2022 lúc 16:04
Cho tam giác ABC vuông tại A có góc B=60 °. Tia phân giác của góc ABCcho tam giác abc vuông tại a có góc b = 60 độ . tia phân giác của góc b cắt ac tại e , kẻ eh vuông góc đc tại h a) chứng minh tam giác abe = tam giác hbe b) hb=hc C) từ H kẻ đường thẳng song song với BE cắt AC ở K .c/m🔺AHK là tam giác đều d) gọi I là giao điểm của BA và HE. Chúng minh IE>EH
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
mà EH là đường cao
nên H là trung điểm của BC
=>HB=HC
d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEI=góc HEC
=>ΔEAI=ΔEHC
=>EI=EC>EH
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có BC = 12cm . B = 60 ° . a ) Giải tam giác ABC . b ) Tính đường cao AH của MBC .
\(a,AB=\cos B\cdot BC=6\left(cm\right)\\ AC=\sqrt{BC^2-AB^2}=6\sqrt{3}\left(cm\right)\\ b,\text{Áp dụng HTL: }AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{3}\left(cm\right)\)
Đúng 3
Bình luận (0)