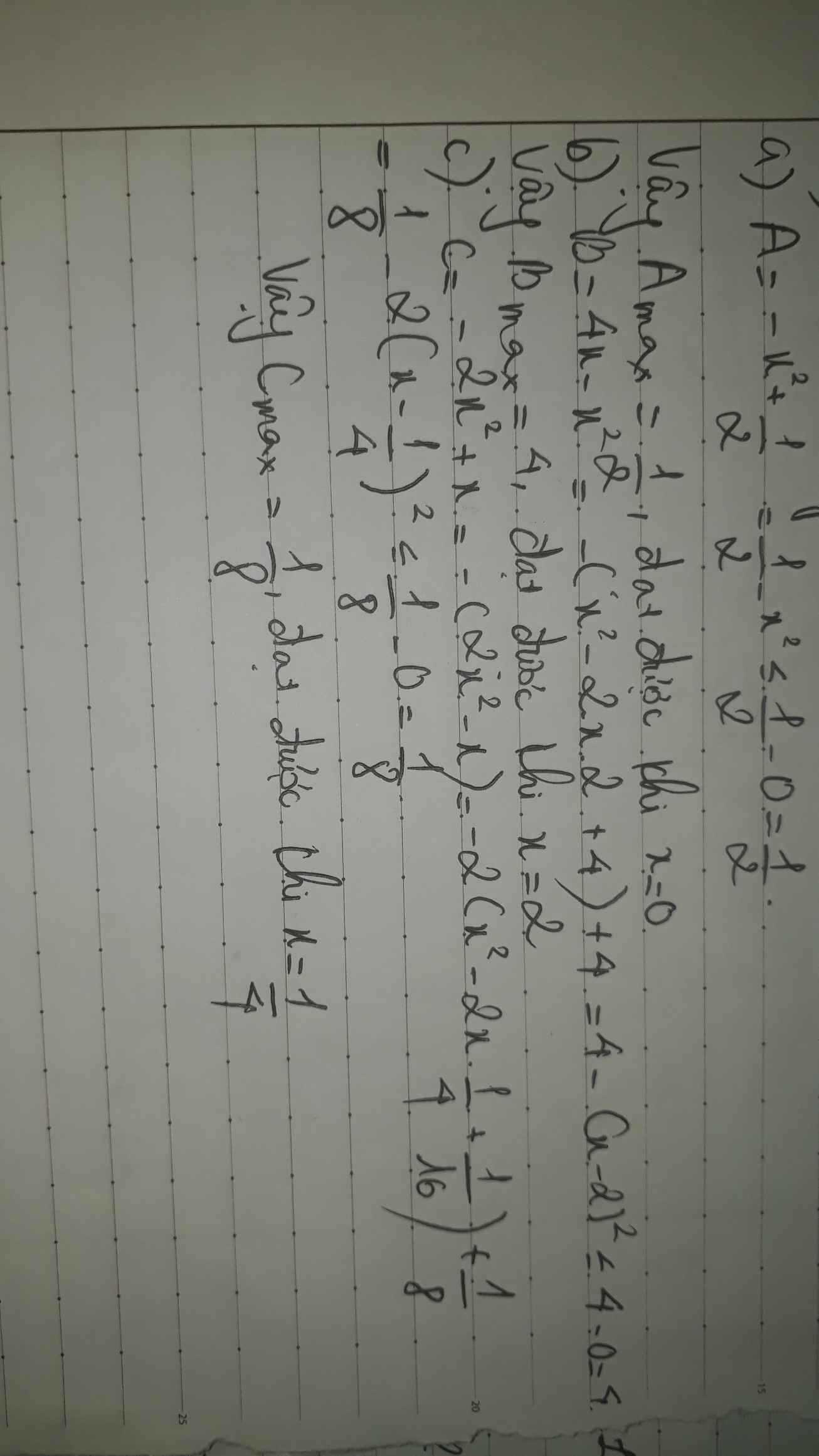`a,2/5 + 3/4`

`= 8/20 + 15/20`

`= 23/20`

`b,2/7 + 5/9`

`= 18/63 + 35/63`

`= 53/63`

`c, 4/7 + 3/4 + 2/7`

`= ( 4/7 + 2/7)+3/4`

`= 6/7 + 3/4`

`= 24/28 + 21/28`

`= 45/28`

`@ yl`

\(\dfrac{2}{5}+\dfrac{3}{4}=\dfrac{8}{20}+\dfrac{15}{20}=\dfrac{23}{20}\)

\(\dfrac{2}{7}+\dfrac{5}{9}=\dfrac{18}{63}+\dfrac{35}{63}=\dfrac{53}{63}\)

\(\dfrac{4}{7}+\dfrac{3}{4}+\dfrac{2}{7}= \left(\dfrac{4}{7}+\dfrac{2}{7}\right)+\dfrac{3}{4}=\dfrac{6}{7}+\dfrac{3}{4}=\dfrac{45}{28}\)

Bạn xem lại đề câu e nhé.

\(A=-x^2+3x-5\)\(=-\dfrac{11}{4}-\left(x^2-2.\dfrac{3}{2}x+\dfrac{9}{4}\right)=-\dfrac{11}{4}-\left(x-\dfrac{3}{2}\right)^2\le-\dfrac{11}{4}\) với mọi x

\(\Rightarrow A_{max}=-\dfrac{11}{4}\Leftrightarrow x-\dfrac{3}{2}=0\Leftrightarrow x=\dfrac{3}{2}\)

\(B=5x-4x^2-3=-\dfrac{23}{16}-\left(4x^2-2.\dfrac{5}{4}.2x+\dfrac{25}{16}\right)\)\(=-\dfrac{23}{16}-\left(2x-\dfrac{5}{4}\right)^2\)\(\le-\dfrac{23}{16}\forall x\)

\(\Rightarrow B_{max}=-\dfrac{23}{16}\Leftrightarrow2x-\dfrac{5}{4}=0\Leftrightarrow x=\dfrac{5}{8}\)

\(C=5-4x-25x^2=\dfrac{129}{25}-\left(25x^2+2.5x.\dfrac{2}{5}+\dfrac{4}{25}\right)\)\(=\dfrac{129}{25}-\left(5x+\dfrac{2}{5}\right)^2\le\dfrac{129}{25}\forall x\)

\(\Rightarrow C_{max}=\dfrac{129}{25}\Leftrightarrow5x+\dfrac{2}{5}=0\Leftrightarrow x=-\dfrac{2}{25}\)

\(D=3x-2x^2=-2\left(x^2-\dfrac{3}{2}x\right)=-2\left(x^2-2.\dfrac{3}{4}x+\dfrac{9}{16}\right)+\dfrac{9}{8}\)\(=\dfrac{9}{8}-2\left(x-\dfrac{3}{4}\right)^2\le\dfrac{9}{8}\) với mọi x

\(\Rightarrow D_{max}=\dfrac{9}{8}\Leftrightarrow x-\dfrac{3}{4}=0\Leftrightarrow x=\dfrac{3}{4}\)

\(E=2+6x-\dfrac{1}{4}x^2=-\dfrac{1}{4}\left(x^2-24x\right)+2=-\dfrac{1}{4}\left(x^2-2.12x+144\right)+38\)\(=38-\dfrac{1}{4}\left(x-12\right)^2\le38\forall x\)

\(\Rightarrow E_{max}=38\Leftrightarrow x-12=0\Leftrightarrow x=12\)

\(F=-5x^2+4x=-5\left(x^2-\dfrac{4}{5}x\right)=-5\left(x^2-2.\dfrac{2}{5}x+\dfrac{4}{25}\right)+\dfrac{4}{5}\)\(=\dfrac{4}{5}-5\left(x-\dfrac{2}{5}\right)^2\le\dfrac{4}{5}\forall x\)

\(\Rightarrow F_{max}=\dfrac{4}{5}\Leftrightarrow x-\dfrac{2}{5}=0\Leftrightarrow x=\dfrac{2}{5}\)

xem lại câu  1 đi

\(5-3x^2+6x=-3x^2+6x+5=-3\left(x^2-2x-5\right)\)

\(=-3\left(x^2-2x+1-6\right)\)

\(=-3\left(x^2-2x+1\right)+18\)

\(=-3\left(x-1\right)^2+18\le18\forall x\)

Dấu = xảy ra khi: \(-3\left(x-1\right)^2=0\Leftrightarrow x=1\)

Vậy : GTLN là 18 tại x = 1

Nguyễn Hoàng Khánh Dương sai rồi nha bạn! Bạn thay x = 1 vào biểu thức xem có ra được giá trị MAX = 18 không???

Gọi biểu thức trên là A.Ta có: \(A=5-3x^2+6x=-3x^2+6x+5\)

\(=-3x^2+6x-3+8\)

\(=-3\left(x^2-2x+1\right)+8\)

\(=-3\left(x-1\right)^2+8\le8\) (do \(-3\left(x-1\right)^2\le0\forall x\))

Dấu "=" xảy ra \(\Leftrightarrow-3\left(x-1\right)^2=0\Leftrightarrow x=1\)

Vậy \(A_{max}=8\Leftrightarrow x=1\)

\(5-3x^2+6x\)

\(=-3\left(x^2-2x-\frac{5}{3}\right)\)

\(=-3\left[\left(x^2-2\cdot x\cdot1+1\right)-\frac{8}{3}\right]\)

\(=-3\left[\left(x-1\right)^2-\frac{8}{3}\right]\)

\(=-3\left(x-1\right)^2+8\)

\(=8-3\left(x-1\right)^2\le8\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow x-1=0\Leftrightarrow x-1\)

Từ đây suy ra tth đúng :))

a) Ta có: \(A=\left|3x+\frac{1}{3}\right|-\frac{1}{4}\ge-\frac{1}{4}\left(\forall x\right)\)

Dấu "=" xảy ra khi: \(\left|3x+\frac{1}{3}\right|=0\Rightarrow x=-\frac{1}{9}\)

Vậy Min(A) = -1/4 khi x = -1/4

b) Ta có: \(\frac{3}{4}-\left|2x-\frac{1}{2}\right|0\le\frac{3}{4}\left(\forall x\right)\)

Dấu "=" xảy ra khi: \(\left|2x-\frac{1}{2}\right|=0\Rightarrow x=\frac{1}{4}\)

Vậy Max(B) = 3/4 khi x = 1/4

a. Vì \(\left|3x+\frac{1}{3}\right|\ge0\forall x\)\(\Rightarrow A=\left|3x+\frac{1}{3}\right|-\frac{1}{4}\ge-\frac{1}{4}\)

Dấu "=" xảy ra \(\Leftrightarrow\left|3x+\frac{1}{3}\right|=0\Leftrightarrow3x+\frac{1}{3}=0\Leftrightarrow x=-\frac{1}{9}\)

Vậy minA = - 1/4 <=> x = - 1/9

b. Vì \(\left|2x-\frac{1}{2}\right|\ge0\forall x\)\(\Rightarrow B=\frac{3}{4}-\left|2x-\frac{1}{2}\right|\le\frac{3}{4}\)

Dấu "=" xảy ra \(\Leftrightarrow\left|2x-\frac{1}{2}\right|=0\Leftrightarrow2x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{4}\)

Vậy maxB = 3/4 <=> x = 1/4

Ta có  \(\left|3x+\frac{1}{3}\right|\ge0\forall x\Rightarrow A=\left|3x+\frac{1}{3}\right|-\frac{1}{4}\ge-\frac{1}{4}\forall x\)

Dấu "=" xảy ra <=> 3x + 1/3 = 0

=> 3x = - 1/3

=> x = -1/9

Vậy GTNN của A là -1/4 khi x = -1/9

Ta có \(\left|2x-\frac{1}{2}\right|\ge0\forall x\Rightarrow B=\frac{3}{4}-\left|2x-\frac{1}{2}\right|\le\frac{3}{4}\forall x\)

Dấu "=" xảy ra <=> 2x - 1/2 = 0

=> 2x = 1/2

=> x = 1/4

Vậy GTLN của B là 3/4 khi x = 1/4

A) \(A=-3x^2+x+1\)

\(A=-3\left(x^2-\dfrac{1}{3}x-\dfrac{1}{3}\right)\)

\(A=-3\left(x^2-2\cdot\dfrac{1}{6}\cdot x+\dfrac{1}{36}-\dfrac{13}{36}\right)\)

\(A=-3\left(x-\dfrac{1}{6}\right)^2+\dfrac{13}{12}\)

Mà: \(-3\left(x-\dfrac{1}{6}\right)^2\le0\forall x\)

\(\Rightarrow A=-3\left(x-\dfrac{1}{6}\right)^2+\dfrac{13}{12}\le\dfrac{13}{12}\forall x\)

Dấu "=" xảy ra khi:

\(x-\dfrac{1}{6}=0\Rightarrow x=\dfrac{1}{6}\)

Vậy: \(A_{max}=\dfrac{13}{12}.khi.x=\dfrac{1}{6}\)

B) \(B=2x^2-8x+1\)

\(B=2\left(x^2-4x+\dfrac{1}{2}\right)\)

\(B=2\left(x^2-4x+4-\dfrac{7}{2}\right)\)

\(B=2\left(x-2\right)^2-7\)

Mà: \(2\left(x-2\right)^2\ge0\forall x\)

\(\Rightarrow B=2\left(x-2\right)^2-7\ge-7\forall x\)

Dấu "=" xảy ra khi:

\(x-2=0\Rightarrow x=2\)

Vậy: \(B_{min}=2.khi.x=2\)

câu a) bạn viết sai đề rồi