Cho hàm số y = x 3 − 3 x có giá trị cực đại và cực tiểu lần lượt là y 1 , y 2 . Mệnh đề nào sau đây đúng?
A. 2 y 1 − y 2 = 6
B. y 1 − y 2 = − 4
C. 2 y 1 − y 2 = − 6
D. y 1 + y 2 = 4
Cho hàm số y=f(x) có bảng biến thiên như sau:
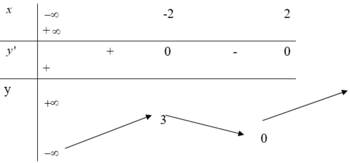
Giá trị cực đại và giá trị cực tiểu của hàm số đã cho lần lượt là?
A. 3 và -2
B. 2 và 0
C. -2 và 2
D. 3 và 0
Giá trị cực đại bằng y(-2)=3 giá trị cực tiểu bằng y(2)=0
Chọn đáp án D.
Cho hàm số y = - x 4 + 2 x 2 + 3 có giá trị cực đại và giá trị cực tiểu lần lượt là y 1 và y 2 Khi đó khẳng định nào sau đây đúng?
A. y 1 + 3 y 2 = 15
B. 2 y 1 - y 2 = 15
C. y 1 - y 2 = 2 3
D. y 1 + y 2 = 12
Cho hàm số y = f x có bảng biến thiên như sau:

Giá trị cực đại và giá trị cực tiểu của hàm số đã cho lần lượt là?
![]()
![]()
![]()
![]()
Cho hàm số y = x 3 - 3 x 2 - 2 . Gọi a,b lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đó. Giá trị của 2 a 2 + b là:
A. -8.
B. -2
C. 2
D. 4
Chọn C
y ' = 3 x 2 - 6 x
y ' = 0 ⇔ x = 0 x = 2
![]()
Cho hàm số y = x 3 - 3 x có giá trị cực đại và cực tiểu lần lượt là y 1 , y 2 . Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho hàm số y = x 3 − 3 x 2 − 2 . Gọi a;b lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đó. Giá trị của 2 a 2 + b bằng
A. -2
B. 4
C. 2
D. -8
Đáp án C
Ta có y ' = 3 x 2 − 6 x = 0 ⇔ x = 0 ⇒ y = − 2 = a x = 2 ⇒ y = − 6 = b
Khi đó 2 a 2 + b = 2
Hàm số y = a x 4 + b x 2 + c đạt cực đại tại A(0;-3) và đạt cực tiểu tại B(-1;-5). Khi đó, giá trị của a, b, c lần lượt là:
A. 2;4;-3
B. -3;-1;-5
C. -2;4;-3
D. 2;-4;-3
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực đại tại x = -2 với giá trị cực đại là 64; đạt cực tiểu tại x = 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng
A. 1
B. 7
C. -17
D. 5
Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d
Từ y ' = 3 a x 2 + 2 b x + c ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c
Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17
Đáp án C
Cho hàm số \(y=x^3-\frac{3}{2}\left(m-2\right)x^2-3\left(m-1\right)x+1\left(1\right)\), m là tham số. Tìm m dương để đồ thị hàm số (1) có giá trị cực đại, giá trị cực tiểu lần lượt là \(y_{CD},y_{CT}\) thỏa mãn \(2y_{CD}+y_{CT}=4\)
Ta có \(y'=3x^2-3\left(m-2\right)x-3\left(m-1\right)\), với mọi \(x\in R\)
\(y'=0\Leftrightarrow x^2-\left(m-2\right)x-m+1=0\Leftrightarrow x_1=-1;x_2=m-1\)
Chú ý rằng với m > 0 thì \(x_1< x_2\). Khi đó hàm số đạt cực đại tại \(x_1=-1\) và đạt cực tiểu tại \(x_2=m-1\). Do đó :
\(y_{CD}=y\left(-1\right)=\frac{3m}{2};y_{CT}=y\left(m-1\right)=-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\)
Từ giả thiết ta có \(2.\frac{3m}{2}-\frac{1}{2}\left(m+2\right)\left(m-1\right)^2+1\Leftrightarrow6m-6-\left(m+2\right)\left(m-1\right)^2=0\)
\(\Leftrightarrow\left(m-1\right)\left(m^2+m-8\right)=0\Leftrightarrow m=1;m=\frac{-1\pm\sqrt{33}}{2}\)
Đối chiếu yêu cầu m > 0, ta có giá trị cần tìm là \(m=1;m=\frac{-1\pm\sqrt{33}}{2}\)