Tìm nguyên hàm F(x) của hàm số f x = sin 2 x , biết F π 6 = 0
A. F x = − 1 2 cos 2 x + π 6
B. F x = cos 2 x − 1 4
C. F x = sin 2 x − 1 4
D. F x = − 1 2 cos 2 x
Những câu hỏi liên quan
Tìm nguyên hàm F(x) của hàm số
f
x
sin
(
π
-
2
x
)
thỏa mãn
F
(
x
2
)
1
Đọc tiếp
Tìm nguyên hàm F(x) của hàm số f x = sin ( π - 2 x ) thỏa mãn F ( x 2 ) = 1
Biết F(x) là một nguyên hàm của hàm số f(x) sin3x.cosx và
F
0
π
. Tìm
F
π
2
. A.
F
π
2
-
1
4
+
π
B.
F
π
2...
Đọc tiếp
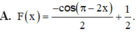
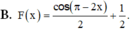
Biết F(x) là một nguyên hàm của hàm số f(x) = sin3x.cosx và F 0 = π . Tìm F π 2 .
A. F π 2 = - 1 4 + π
B. F π 2 = 1 4 + π
C. F π 2 = - π
D. F π 2 = π
Biết F(x) là một nguyên hàm của hàm số
f
x
e
-
x
+
sin
x
thỏa mãn F(0) 0. Tìm F(x)?
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f x = e - x + sin x thỏa mãn F(0) = 0. Tìm F(x)?
Đáp án A
Phương pháp :
Sử dụng bảng nguyên hàm cơ bản.
Cách giải:
Ta có:
Đúng 0
Bình luận (0)
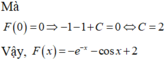
Biết F(x) là một nguyên hàm của hàm số f(x)=sin2 x+cosx. Giá trị F(π/2)-F(0) bằng
A. 2.
B. 1
C. -1
D. 4.
biết F(x) là một nguyên hàm của hàm số f(x)=sin²2x*sinx. tính F(x)
Xem chi tiết
f(x)=4sin2x.cos2x.sinx=4(1-cos2x)cos2x.sinx=(4cos4x-4cos2x)(-sinx)
Đặt u=cosx ---> F(x)=(4/5)cos5x-(4/3)cos3x+C
Đúng 0
Bình luận (1)
Biết F(x) là một nguyên hàm của hàm số f(x) sin x và đồ thị hàm số y F(x) đi qua điểm M(0;1) . Tính
F
π
2
. A.
F
π
2
0
B.
F
π
2
1
C.
F
π
2
2
D.
F...
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f(x) = sin x và đồ thị hàm số y = F(x) đi qua điểm M(0;1) . Tính F π 2 .
A. F π 2 = 0
B. F π 2 = 1
C. F π 2 = 2
D. F π 2 = - 1
Tìm nguyên hàm của hàm số
f
(
x
)
(
sin
x
+
c
o
s
x
)
2
A.
∫
f
(
x
)
d
x
x
+
1
2
c
o
s...
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = ( sin x + c o s x ) 2
A. ∫ f ( x ) d x = x + 1 2 c o s 2 x + C
B. ∫ f ( x ) d x = 1 2 c o s 2 x + C
C. ∫ f ( x ) d x = - 1 2 c o s 2 x + C
D. ∫ f ( x ) d x = x - 1 2 c o s 2 x + C
Cho hàm số F(x) là một nguyên hàm của hàm số
f
(
x
)
2
cos
x
-
1
sin
2
x
trên khoảng
0
;
π
. Biết rằng giá trị lớn nhất của F(x) trên khoảng
0...
Đọc tiếp
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?
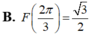
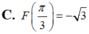
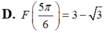
Biết F(x) là một nguyên hàm của hàm số f(x) = sin 2x + cosx. Giá trị F π 2 - F ( 0 ) bằng
A. 2.
B. 1.
C. -1.
D. 4.
Câu 1 : Tính thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y = x3 , y = 0, x=0, x=1 quanh trục hoành
Câu 2 : Biết F(x) là một nguyên hàm của hàm f(x) = sin2x và F(π/4) = 1. Tính F(π/6)
1.
\(V=\pi\int\limits^1_0x^6dx=\dfrac{\pi x^7}{7}|^1_0=\dfrac{\pi}{7}\)
2.
\(F\left(x\right)=\int sin2xdx=-\dfrac{1}{2}cos2x+C\)
\(f\left(\dfrac{\pi}{4}\right)=1\Leftrightarrow-\dfrac{1}{2}cos\dfrac{\pi}{2}+C=1\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}cos2x+1\Rightarrow F\left(\dfrac{\pi}{6}\right)=\dfrac{3}{4}\)
Đúng 2
Bình luận (0)