Xét các mệnh đề sau:
(1) Nếu hàm số f x = x thì f ' x = 0 .
(2) Nếu hàm số f x = x 2017 thì f ' x = 0 .
(3) Nếu hàm số f x = x 2 - 3 x + 1 thì phương trình f ' x = 0 có 3 nghiệm phân biệt.
A. (1), (2)
B. (2), (3)
C. (1), (2), (3)
D. (2)
Cho hàm số có f đạo hàm trên khoảng I. Xét các mệnh đề sau:
(I). Nếu , thì hàm f '(x) < 0 "x ∈ I số nghịch biến trên I
(II). Nếu , f '(x) ≤ 0 "x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số nghịch biến trên I
(III). Nếu , thì hàm f '( x) ≤ 0 "x ∈ I số nghịch biến trên khoảng I
(IV). Nếu , f '(x) ≤ 0 "x ∈ I và f '(x) = 0 tại vô số điểm trên thì hàm I số không f thể nghịch biến trên khoảng I
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
A. I, II và IV đúng, còn III sai.
B. I, II, III và IV đúng.
C. I và II đúng, còn III và IV sai.
D. I, II và III đúng, còn IV sai.
Đáp án là C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I
Cho hàm số y=f(x) có đạo hàm đến cấp 2 trên khoảng (a;b) có chứa điểm x o Xét các mệnh đề sau:
(I): Nếu f ' ( x ) = 0 f ' ' ( x ) > 0 thì x = x o là điểm cực tiểu của hàm số.
(II): Nếu f ' ( x ) = 0 f ' ' ( x ) < 0 thì x = x o là điểm cực đại của hàm số.
(III): Nếu f ' ( x ) = 0 f ' ' ( x ) = 0 thì x = x o không là điểm cực trị của hàm số.
Trong các mệnh đề trên, có bao nhiêu mệnh đề sai?
A.0
B. 1
C. 2
D. 3
Cho hàm số y = f (x) có đạo hàm trên khoảng I. Xét các mệnh đề sau
(I). Nếu f’(x) ≥ 0, ∀ x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số f đồng biến trên I.
(II). Nếu f’(x) ≤ 0, ∀ x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số f nghịch biến trên I.
(III). Nếu f’(x) ≤ 0, ∀ x ∈ I thì hàm số f nghịch biến trên khoảng I.
(IV). Nếu f’(x) ≤ 0, ∀ x ∈ I và f’(x) = 0 tại vô số điểm trên I thì hàm số f không thể nghịch biến trên khoảng I.
Trong các mệnh đề trên, mệnh đề nào đúng, mệnh đề nào sai?
A. I và II đúng, còn III và IV sai
B. I, II và III đúng, còn IV sai
C. I, II và IV đúng, còn III sai
D. Cả I, II, III và IV đúng
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
Cho hàm số y = f x xác định, có đạo hàm trên đoạn a ; b (với a < b ). Xét các mệnh đề sau:
i) Nếu f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên khoảng a ; b .
ii) Nếu phương trình f ' ( x ) = 0 có nghiệm x 0 thì f ' ( x ) đổi dấu từ dương sang âm khi qua x 0 .
iii) Nếu f ' x ≤ 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
Số mệnh đề đúng trong các mệnh đề trên là:
A. 2
B. 3
C. 0
D. 1
Chọn D
i) Đúng.
ii) Sai, ví dụ: Xét hàm số
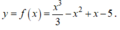
Ta có f ' x = x 2 - 2 x + 1 .
Cho f ' ( x ) ⇔ x = 1 .
Khi đó phương trình f ' ( x ) = 0 có nghiệm x 0 = 1 nhưng đây là nghiệm kép nên không đổi dấu khi qua x 0 .
iii) Sai, vì: Thiếu điều kiện f ' ( x ) = 0 chỉ tại một số hữu hạn điểm.
Vậy có 1 mệnh đề đúng.
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Đáp án A
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f (x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f ( x ) = x ta có D= R nên hàm số f(x) liên tục trên R.
Nhưng ta có l i m x → 0 + f ( x ) - f ( 0 ) x - 0 = l i m x → 0 + x - 0 x - 0 = l i m x → 0 + x - 0 x - 0 = 1 l i m x → 0 - f ( x ) - f ( 0 ) x - 0 = l i m x → 0 - x - 0 x - 0 = l i m x → 0 - - x - 0 x - 0 = - 1
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
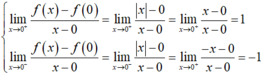
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
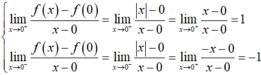
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai .
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó. Đây là mệnh đề sai.
- Ví dụ: Lấy hàm f(x) = |x| ta có tập xác định D = R . +)Với mọi
x
0
≠ 0 thì 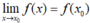
+)Lại có:
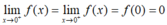
→ Nên hàm số f(x) liên tục trên R.
+) Nhưng ta có:
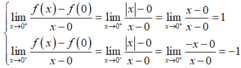
→ Nên hàm số không có đạo hàm tại x = 0.
→ Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vì (1) là mệnh đề đúng nên ta suy ra : Nếu f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.
Cho hàm số y = f (x) có đạo hàm trên R. Xét tính đúng sai của các mệnh đề sau.
(I): Nếu f’(x) > 0 trên khoảng (x0–h;x0) và f’(x) < 0 trên khoảng (x0;x0+h) (h>0) thì hàm số đạt cực đại tại điểm x0
(II): Nếu hàm số đạt cực đại tại điểm x0 thì tồn tại các khoảng (x0–h;x0), (x0;x0+h) (h>0) sao cho f’(x) > 0 trên khoảng (x0–h;x0) và f’(x) < 0 trên khoảng (x0;x0+h)
A. Cả (I) và (II) cùng sai
B. Mệnh đề (I) đúng, mệnh đề (II) sai
C. Mệnh đề (I) sai, mệnh đề (II) đúng
D. Cả (I) và (II) cùng đúng