Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y2x2�2�2 và đường thẳng (d) có phương trình y2(m−1)x−m+�2(�−1)�−�+ 1, trong đó m là tham số. a, Vẽ parabol (P).b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y2x2�2�2 và đường thẳng (d) có phương trình y2(m−1)x−m+�2(�−1)�−�+ 1, trong đó m là tham số. a, Vẽ parabol (P).b, Xác đị...
Đọc tiếp
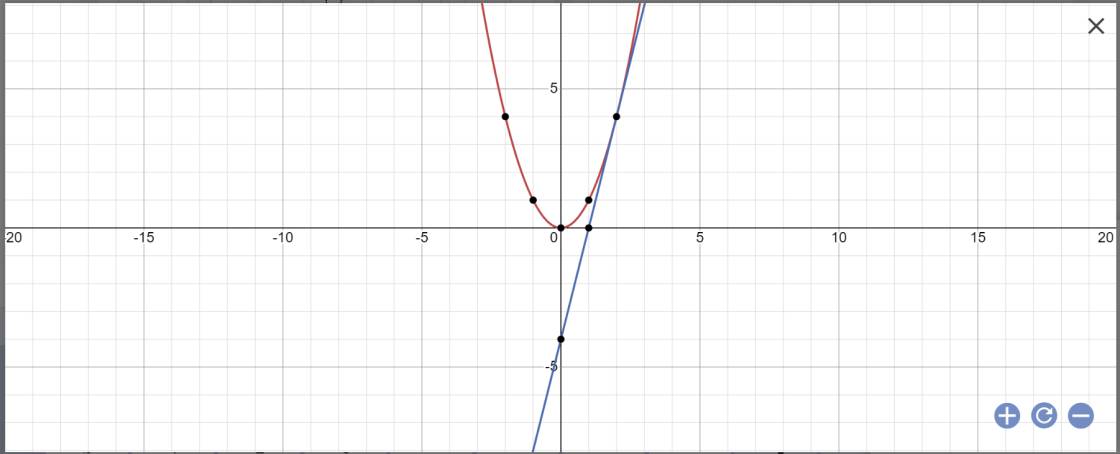
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y=2x2�=2�2 và đường thẳng (d) có phương trình y=2(m−1)x−m+�=2(�−1)�−�+
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình
y=2x2�=2�2 và đường thẳng (d) có phương trình y=2(m−1)x−m+�=2(�−1)�−�+
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định