Cho phương trình 3 x = a . 3 x   cos   ( π x ) - 9 . Có bao nhiêu giá trị thực của tham số a thuộc đoạn [ -2018; 2018] để phương trình đã cho có đúng một nghiệm thực?

A. 1

B. 2018

C. 0

D. 2

Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 2018 để phương trình m + m + e x = e x có nghiệm thực.

Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 2018 để phương trình m + m + e x = e x có nghiệm thực.

A. 2016

B. 2017.

C. 2018

D. 2019

Hỏi có bao nhiêu giá trị nguyên của tham số thực m  để phương trình logarit  log 3 2 x + log 3 2 x + 1 - 2 m - 1 = 0 có nghiệm thuộc đoạn  1 ; 3 3

A. 3

B. 2

C. 1

D. 0

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-20;20] để bất phương trình 2 2 x + 1 - 12 m . 2 x - 1 + 5 m 2 - 10 < 0  có nghiệm thực?

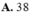
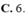
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn - 20 ; 20  để bất phương trình 2 2 x + 1 - 12 m . 2 x - 1 + 5 m 2 - 10 < 0  có nghiệm thực?

A. 38

B. 3

C. 6.

D. 32

Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [ - 2018 ; 2018 ]  để hàm số y   =   f x   =   x + 1 ln x   + 2 - m x  đồng biến trên khoảng 0 ; e 2 .

A.2016

B.2022

C.2014

D.2023